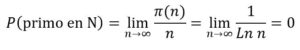Laplace escribió el libro Teoría Analítica de las Probabilidades (1812), en el que desarrollaba el Cálculo de Probabilidades en términos del Cálculo Infinitesimal, pero formuló una definición del concepto de probabilidad inspirado en el contexto en el que había aparecido en su origen con el estudio de los juegos de azar. Definió la probabilidad de se produzca un suceso como el cociente entre el número de casos favorables en los que aparece el suceso dividido entre el número de casos en los que es posible que suceda. La definición se aplica directamente cuando siempre que podamos contar el número de casos, es decir para conjuntos numerables. Ni Laplace ni sus sucesores se pararon a estudiar la probabilidad cuando los casos favorables, los posibles o ambos son infinitos numerables. Estas cuestiones, aunque son sencillas, no se plantaron hasta que en la matemática empezaron a manejar con naturalidad los conjuntos infinitos.
Primero. Calcular la probabilidad de extraer un número par elegido al azar del conjunto de números naturales menores que 1000: A = {1, 2, 3, 4, 5, .., 1000}
Respuesta: En A hay 500 números pares menores o iguales que 1000, luego: P = 500/1000 = 0,5
Segundo. Calcular la probabilidad de extraer un número par elegido al azar del conjunto A de los números naturales menor que 1.001.
Respuesta: En A hay 500 números pares menores o iguales que 1001. Por lo tanto: P = 500/1001 = 0,4995
Tercero. Calcular la Probabilidad de extraer un número par elegido al azar del conjunto N = {1, 2, 3, 4, 5, .., n, … } (infinito) de los números naturales.
Respuesta: En el conjunto N de los números naturales hay infinitos números pares e infinitos números naturales. Si aplicamos la definición de probabilidad de Laplace de relación entre números de casos favorables entre número de casos posibles. La probabilidad será: P = ∞/∞ que es indeterminado. Pero aquí podemos aplicar un concepto de probabilidad como límite de las frecuencias relativas. Numero pares menores que 1000, si no consideramos el 0, hay 500, menores de un millón hay 500.000, menores de mil millones hay 500.000.000,

Las frecuencias cuando n tiende a infinito también serán 0,5. Probabilidad de extraer un número par del conjunto N será: P = 0,5
Cuarto. Calcular la probabilidad de extraer una potencia de 2 del conjunto N de los números naturales menores que 1.000 (consideraremos que 1 no es potencia de 2).
Respuesta: Observemos que 29 = 512 y 210 =1024. Luego hay de 0 a 1.000 hay nueve potencias de dos. Aplicando la definición de Laplace: P = 9/1.000 = 0,009
Quinto.- Calcular la probabilidad de extraer una potencia de 2 del conjunto N de los números naturales menor que 1.000.000.
Respuesta: En este caso utilizaremos logaritmos:
2n ≤ 1.000.000 ⇒ n ≤ log2(1000000) =
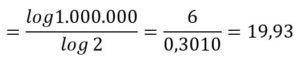
Luego hay 19 potencias de dos menores que 1.000.000, por lo tanto, aplicando la definición de Laplace:
P = 19/1.000.000
(Podemos observar que 219 = 524288 y 220 =1048576, luego entre 19/1.000.000)
Sexto. Calcular la probabilidad de extraer una potencia de 5 del conjunto N de los números naturales menor que 1.000.000
Respuesta: Análogamente al ejercicio anterior:
5n ≤ 1000000 ⇒ n ≤ log5(1000000) =
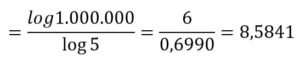
Hay 8 potencias de 5 menores que 1.000.000, po lo tanto: P = 8/1.000.000 = 0,000008
Séptimo: Calcular la probabilidad de extraer una potencia de 2 del conjunto completo N de los números naturales
Respuesta: En el conjunto N de los números naturales hay infinitas potencias de dos e infinitos números naturales. Si aplicamos la definición de probabilidad de Laplace dividiendo el número de casos favorables entre número de casos posibles. La probabilidad será: P = ∞/∞ que es una indeterminación.
Pero el número potencias de dos menores que 210, si no consideramos el 1 como potencia de dos, es 10, el de menores que 220, es 20 y, en general, el de menores que 2n, es n. Es decir,
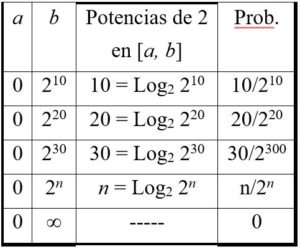
Por lo tanto:
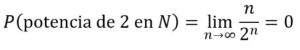
Octavo.- Calcular la probabilidad de extraer una potencia de 5 del conjunto completo N de los números naturales
Respuesta: Análogo al anterior:
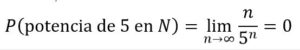
Noveno.- Calcular la probabilidad de extraer un número primo del conjunto N de los números naturales menor que 1.000.000.
Respuesta: La Teorema sobre la distribución de los números primos dice que el número de números primos menores que n, que se designa con π(n) es:
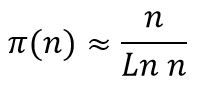
Luego P (obtener un primo menor que n) = π(n)/n = 1/Ln n. Y para n = 1.000.000:
![]()
Décimo.- Calcular la probabilidad de extraer un número primo en N
Respuesta: