
Ch. Huygens (629-1695) publicó en 1656 el primer tratado sobre el estudio matemático en los juegos de azar, lo escribió en latín, y lo llamó De Ratiociniis in Ludo Aleae [El raciocinio en los juegos de azar] En él introdujo el concepto de Esperanza Matemática para variables aleatorias que tomaban dos o tres valores. Este concepto lo definió como la ganancia media esperada que se obtendría si el juego se repitiera muchas veces. También resolvió el Problema de los Puntos, que era el problema que se planteaba con el reparto de apuestas entre dos jugadores cuando se interrumpía un juego ya comenzado y utilizó un método semejante al empleado por B. Pascal (1623-1662) y P. Fermat (1601-1665). Huygens amplió el Problema de los Puntos para hacer el reparto en el caso de tres jugadores y se centró en el estudio de los juegos de azar y estableció los fundamentos matemáticos de las apuestas. Sentó las bases de la ventaja matemática de la banca y permitía calcular el beneficio esperado de la explotación empresarial del juego por casinos o casas de juego en diferentes juegos de azar.
Huygens se planteó el estudio del azar como un problema físico que había que resolver y, aunque hizo aportaciones brillantes, no definió el concepto de probabilidad, ni otras ideas con el grado de abstracción suficiente como para construir una teoría matemática amplia y consistente con la que estudiar otros fenómenos en los que intervenía el azar.

El matemático suizo Jacob Bernoulli (1665-1705) descubrió la Ley de los Grandes Números, que dio a conocer en su obra, también escrita en latín, Ars Conjectandi [El arte de la conjetura] en 1713. La Ley de los Grandes Números es un resultado fundamental de la Teoría de Probabilidades. Afirma que si repetimos muchas veces (tendiendo al infinito) un mismo experimento, la frecuencia de que ocurra un suceso determinado tiende a estabilizarse en un valor una constante. La Ley de los Grandes Números superó los límites de una teoría del azar confinada en el territorio de los juegos de dados, de cartas y estudio de las apuestas, ya que relacionaba la repetición de experimentos con la repetición de acontecimientos recogidos en cada año en las estadísticas de tablas de nacimientos y defunciones como las que publicó John Graunt ( 1620-1664) en un tratado en el que recopilaba una serie de observaciones políticas y naturales acaecidas entre 1.604 y 1.661 y estudiaba la influencia de las causas naturales, sociales y políticas de diferentes acontecimientos.
La idea, aunque no fue del agrado de algunos matemáticos, que se resistían a introducir términos imprecisos, como número grande de veces, tiende a estabilizarse, etc. ¿Era un paso al límite? Esa idea juega a favor de que Laplace utilizara Cálculo Infinitesimal en el Cálculo de Probabilidades. Actualmente la Ley de los Grandes Números se conoce como Ley de Bernoulli y es una idea básica en la teoría del muestreo moderno.
Ni Ch. Huygens ni J. Bernoulli proporcionaron un concepto básico con el que estudiar el azar de forma abstracta para que pudiera convertirse en una teoría matemática. Huygens por quedare pegado al estudio de los juegos de azar y Bernoulli porque, aunque su resultado fue importantísimo, en última instancia, no e posible repetir un experimento infinitas veces para comprobarlo y la idea de que la frecuencia de que ocurra un suceso determinado en un experimento tienda a hacia un valor constante parece ir en contra de la propia idea de azar..
El primero que proporcionó un concepto medible para abordar los diferentes juegos y capaz de describir los fenómenos que dependen del azar fue P.S. Laplace (1749-1927) en su Teoría Analítica de las Probabilidades (1812), donde expuso los principios del Cálculo de Probabilidades y mostró muchas aplicaciones de este cálculo, que él llamó geometría del azar.
Esta la obra presentó los recursos del Cálculo infinitesimal aplicados al estudio de los fenómenos aleatorios. Introdujo las funciones generatrices, propuso métodos para estudiar la distribución de los errores en las mediciones en física y el método de mínimos cuadrados. Aplicó Cálculo de Probabilidades como método para determinar la causa más probable de un suceso (Teorema de Bayes). Aplicó el Cálculo de Probabilidades a tablas de mortalidad, resultados de elecciones, etc. En la obra recoge los trabajos de cuarenta años de investigaciones y Memorias sobre esta materia.

Laplace expresó de forma sencilla un concepto abstracto, el concepto de probabilidad, en torno al cual se habían de formular los resultados obtenidos hasta entonces sobre la teoría del azar y que se llamaría Teoría de Probabilidades. Laplace formuló una definición sencilla derivada de los juegos de azar y era que la probabilidad de un suceso era el cociente entre el número de casos favorables en los que puede acaecer el suceso y el de casos posibles que puede producir el experimento.
Laplace concedió mucha importancia a la Teoría de Probabilidades y destacaba que le parecía asombroso que una teoría que había surgido por consideraciones sobre juegos de azar se había convertido en una herramienta importante del conocimiento humano. Ya que muchas cuestiones del comportamiento humano se reducían a problemas de probabilidad. Consideraba que la probabilidad era solamente el sentido común expresado con números.
Su definición era intuitiva clara y útil, pero suponía que todos los casos eran igualmente posibles lo que introducía una creencia apriorística, ¿Cómo saber a priori si todos los sucesos eran igualmente posibles? El concepto de sucesos igualmente posibles se da por supuesto en la definición de probabilidad.
No obstante, Laplace añadía que si todos los casos no fueran igualmente posibles, se debían determinar sus posibilidades respectivas, y, entonces, la probabilidad del suceso sería la suma de las probabilidades de cada caso favorable. La definición laplaciana de probabilidad era puramente subjetiva y no hacía ninguna concesión a la experiencia real a partir del análisis de las frecuencias relativas.
En los juegos de azar, como sucedía en los juegos de dados, era posible contar los casos favorables y los posibles. En los problemas de probabilidad con conjuntos numéricos era más difícil y en los problemas geométricos, en los que intervenía el continuo, surgían conjuntos no numerables que no se podía contar, sino que se debía medir y esto producía ciertas situaciones y paradójicas.
Dependiendo de la medida que utilicemos para calcular la probabilidad en Geometría (longitud, área, etc.) el resultado podía ser distinto. Van Fraassen, B.C, en su libro Laws and Symmetry (1989) recoge la siguiente paradoja que he tomado del artículo de G. Ruiz Garzón en la revista SUMA (2001), titulado Sobre la utilidad de la Geometría en la enseñanza de la Probabilidad .
PROBLEMA: Una fundición fabrica cubos de hierro macizos, C, de arista menor o igual que 2 cm ¿Cuál es la probabilidad de que un cubo C1, construido en esa fundición, tenga una arista menor o igual que 1 cm?
Primera solución: Como suponemos que las medidas de los cubos tienen tamaños al azar, fabricará cubos cuyas aristas posibles pertenecen al intervalo real (0,2), las aristas y las aristas favorables tendrán medida comprendidas en (0,1)
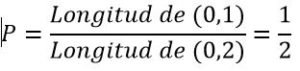
Segunda solución: También podemos tomar como medida el volumen de hierro gastado en la construcción de cada cubo. Los volúmenes favorables serán los menores o iguales que 1 y los posibles menores o iguales que 8.
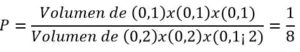
Tercera solución: También podemos tomar como medida la superficie de la cara de los cubos, entonces, las áreas favorables serán las menores o iguales que 1 y las posibles menores o iguales que 4.
![]()
Lo que da tres posibles probabilidades para el problema propuesto. La paradoja se produce porque, en realidad no se trata de un problema, sino de tres ya que el experimento aleatorio ligado al azar es diferente, y por consiguiente los resultados son distintos si los datos que se toman al azar líneas, superficies y volúmenes.
A finales del siglo XIX y comienzos del siglo XX se realizó una revisión de los fundamentos de las matemáticas encabezada por D. Hilbert (1862-1943) y algunos matemáticos se propusieron la via frecuentista, que era una vista atrás hacia la Ley de los Grandes Números. Si un experimento aleatorio pudiera repetirse infinitas veces en las mismas condiciones, entonces la probabilidad de un suceso aleatorio sería el límite al que tendería su frecuencia relativa.
Como es obvio, el sistema tenía sus detractores. En primer lugar, como hemos apuntado anteriemente, no podemos repetir infinitas veces un experimento, así que en la práctica debemos contentarnos con una estimación cercana de la probabilidad. Otra crítica que se le hizo en contra de sus validez lógica era que se estaban manejando la idea de que una sucesiones aleatoria tenía un límite y la idea de que la sucesión aleatoria de estabilizara contradecía el carácter aleatorio de la sucesión.

El físico austrohúngaro R. von Mises (1883-1953), en su libro Probabilidad, Estadística y Verdad (1928), desarrolló la Teoría de Probabilidades objetiva o de frecuencias.
Tampoco la probabilidad podía utilizarse para elaborar una Teoría de Probabilidades libre de paradojas, ya que las observaciones reales no pueden utilizarse para definir un concepto abstracto ni justificar una convergencia. No obstante, aunque la probabilidad no podía definirse sobre el concepto intuitivo de convergencia, la frecuencia relativa tenía unas propiedades que serían utilizadas por A. Kolmogorov (1903-1987) para dar una definición formal de la probabilidad.

Kolmogorov, en su libro Fundamentos de la Teoría de la Probabilidad (1933) expresó la Teoría Axiomática de Probabilidades. La redactó aprovechando los recursos de la teoría de la medida, y definiendo la probabilidad como una medida positiva. En particular, Kolmogorov resolvió parcialmente el Sexto Problema de Hilbert, de los ventitrés propuestos por el matemático alemán en el Congreso de París de 1900, sobre la axiomatización de la física. La definición es la siguiente:
Dado un experimento aleatorio, si llamamos E al espacio muestral (o conjunto de todos los resultados posibles) y A y B son sucesos (o subconjuntos de E):
Definición: Para cada suceso A, perteneciente a un espacio muestral E, se define la probabilidad de A (P(A)) como una función medida de P: P(E) → R, que cumple los siguientes axiomas: (P(E), el conjunto de todos los subconjuntos de E)
- La probabilidad de cualquier suceso, A es siempre mayor o igual que cero: P(A)≥0
- La probabilidad del espacio muestral es 1: P(E)=1
- La probabilidad de la unión de sucesos incompatibles es igual a la suma de las probabilidades de cada uno de ellos. En el caso de dos sucesos incompatibles A, B incompatibles (A∩B=Ø) se expresa que P(AUB) = P(A) + P(B)




