La suma de la sucesión de los números naturales y de suma de sus inversos para el producto pertenecen al tipo de problemas populares y profundos de las matemáticas. Sobre la suma de una sucesión de los números naturales se recoge una anécdota sobre el niño prodigio de las matemáticas C.F. Gauss (1777-1855) en la que su maestro, seguramente para tener a los niños callados y entretenido, les propuso el problema de calcular la suma de cien primeros números, el joven Gauss que a la sazón tenía nueve años, respondió casi inmediatamente: 1 + 2 + 3 + … + 99 + 100 = 5050. Gauss se dio cuenta de que la suma de los pares de números equidistantes de los extremos suman 101, así 1 + 100, 2 + 99, 3 + 98,… suman 101, y como de uno a cien hay cincuenta pares, la suma será 50 × 101 = 5050.
De esta anécdota no hay testimonio histórico, pertenece al tipo de relatos semejantes al descubrimiento de la armonía musical por Pitágoras, al Principio de Arquímedes y su bañera o la Ley de Gravitación y la manzana de Newton, pero lo cierto es que la suma de sucesiones de números naturales y la suma de sus inversos para el producto han fascinado a los matemáticos y los conocimientos sobre estas sumas se han ido ampliando a lo largo de la historia.
La serie armónica debe su nombre a que la longitud de onda de los armónicos de una cuerda que vibra (supongamos que tiene longitud unidad) son proporcionales a las fracciones unitarias, que son los sumandos de la serie armónica:
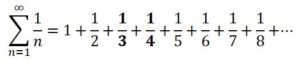N. de Oresme, (1323 –1382), en 1350, fue el primero que demostró que la serie armónica era divergente. Siglos después P. Mengoli (1626-1686), alumno de B Cavalieri (1598-1647) abordó una nueva demostración, a la que siguieron las de los hermanos Johann y Jacob Bernoulli a comienzos del siglo XVIII.
Desde que en el siglo XIII se comenzaran a utilizar Los métodos aritméticos y algebraicos los procedimientos geométricos fueron sustituidos por los nuevos recursos que proporcionaban los cálculos aritméticos. En este artículo vamos a aproximar al cálculo estudio de la serie armónica y la serie armónica alternada con los métodos clásicos del cálculo que se desarrollaron hasta el siglo XVIII. En la actualidad, la mayoría de los matemáticos se aproximarían a la resolución de un problema de este estilo con la ayuda de programas informáticos de los ordenadores ¿Quién hace en la actualidad matemática con lápiz y papel?
Nicolás de Oresme demostró que la serie armónica era divergente en un momento en el que la aritmética y el sistema de numeración posicional se habían afianzado en el campo de las matemáticas, haciendo uso de las suma de los términos de una progresión geométrica y de la siguiente propiedad de las fracciones:
Asociando convenientemente sus sumandos de la serie armónica y aplicando esa propiedad, resultaba:
Esta serie no estaba acotada, ya que cada uno de los corchetes arrojaba una suma mayor que 1/2 . Con lo que:
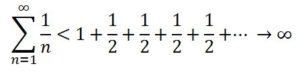
Con la aparición de los logaritmos a comienzos del siglo XVI en el libro de J. Napier (1550-1617) Mirifici Logarithmorum Canonis Descriptio (1614), los logaritmos se usaron masivamente para facilitar el cálculo y fueron utilizados por J .Kepler (1571-1630) para elaborar sus Tablas Rudolfinas (1623). Gracias a los logaritmos se profundizó en el tipo de divergencia que realmente tendía infinito, pero muy despacio. Se demostró que:
Como (1) acota a una sucesión creciente, sumando (1) desde i=1 hasta un valor de n:
Este resultado fue obtenido por L. Euler (1701-1783) en sus Institutiones Calculi Integralis (1768-1770) pero fue L. Mascheroni (1750-1800) en sus Adnotationes ad calculum integrale Euleri (1790) el que publicó el cálculo de la constante de Euler-Mascheroni. Construyó la serie:
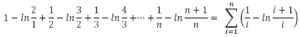Es una serie alternada (sumandos alternativamente positivos y negativos) con valores decrecientes en valor absoluto y que el término general tiende a cero, por lo tanto, por el criterio de convergencia de Leibniz es convergente y la podemos reordenar sin que cambie su suma:
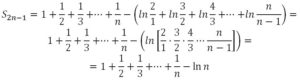
Y e sigue que (llamando Hn a la suma de los n primeros rérminos de la serie armónica):
Mascheroni calculó esa constante que era γ=0,57721566…
El uso de ordenadores en la investigación matemática proporcionó una ayuda a la aproximación de un problema, ya que el cálculo que permite experimentar y seleccionar las hipótesis útiles, para la resolución de problemas. Calcular esta contante. A continuación se dan los resultados de S10, S100, S1.000 , …, S1000000 de la serie armónica alternada junto a Ln 10, Ln 100, Ln 1.000, …, Ln 1.000.000 y sus diferencias. Se han calculado con el programa Derive y se observa la lenta aproximación al valor de γ:
