Para Aristóteles las matemáticas y la física tenían temas de estudio y objetivos diferentes, puesto que, según él, las matemáticas se ocupaban de ideas abstractas y poco podían a ayudar a la física para descubrir la esencia de las cosas concretas en el mundo físico. Aristóteles había considerado una fantasía pitagórica pensar que los números formaban parte de la esencia de las cosas y no aceptaba que los números fueran causa de ninguna manifestación del comportamiento de los objetos naturales.
Cuando en la ciencia moderna se aplicaron las matemáticas al estudio de la realidad observable, no se intentaba descubrir su esencia (la ciencia no busca la esencia de los objetos materiales) sólo trataba de describir su comportamiento. De hecho, Galileo no estudió la caída de los graves considerando si el cuerpo, en su caída, buscaba el lugar que le correspondía por su naturaleza, que le impulsaba de forma necesaria a llegar a su estado permanente de reposo, sino que describió, de forma precisa, cómo variaba la velocidad del grave durante su caída. Las matemáticas aplicadas a la física no se preguntaban por la esencia de las cosas, sino que perseguían conseguir una descripción puntual y exacta de la realidad observable.
En este sentido se puede decir que la ciencia aristotélica trataba de conocer las cosas por sus causas, lo que significaba conocer las cuatro causas para llegar a entender el por qué de las cosas. ¿Por qué existía ese objeto? ¿Por qué se movía? Sin embargo, la ciencia moderna se preguntaba cómo eran y cómo se comportaban las cosas, lo que suponía un cambio de los objetivos del conocimiento con respecto a la filosofía clásica. La ciencia moderna, aparecida en el siglo XVI, supuso un cambio fundamental en el cual los científicos pasaron de preguntarse el por qué a investigar sobre el cómo.
Podemos decir que Galileo fue el primer científico que aplicó las matemáticas al estudio del mundo sublunar, que era la parte del cosmos donde el hombre vivía. Sin embargo, las matemáticas, más particularmente la geometría, se aplicaron desde la antigüedad al estudio del movimiento de los astros.
A continuación, veremos algunas razones por las que las matemáticas no se utilizaron inicialmente en el estudio de los fenómenos naturales que se daban en la Tierra y se emplearon desde la antigüedad para el estudio de los movimientos de los cuerpos celestes. La primera razón es la consideración diferente que tenían, en la cosmología aristotélica, el mundo supralunar y el mundo sublunar.
El cosmos de la filosofía Aristotélica estaba formado por la Tierra, que era una esfera inmóvil situada en el centro del universo y, alrededor de ella giraban las estrellas, los planetas y los demás astros alojados en esferas concéntricas transparentes con centro en la Tierra, que los transportaban girando en círculos perfectos eternamente.
La cosmología de Aristóteles tenía como punto de partida la estructura platónica propuesta por Eudoxo de Cnido (390-337), que fue discípulo de Platón (427-347 a. C.) en la Academia, el cual, recogiendo la idea platónica de que el círculo y la esfera eran las formas más perfectas y hermosas, imaginó que el cosmos perfecto y ordenado por un Demiurgo, debía tener forma esférica, estar dotado de un movimiento de rotación uniforme en torno a un centro, que debía se la Tierra.
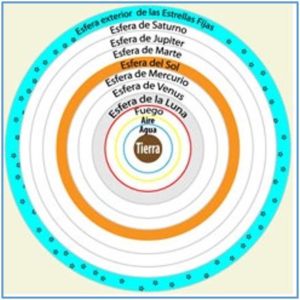
Eudoxo representó el movimiento los cuerpos celestes considerando que estaban incrustados en esferas cristalinas, transparentes y homocéntricas, con centro en la Tierra, que giraban con ejes diferentes, y necesitó treinta y tres esferas, descontando la de las estrellas fijas para describir el movimiento de los astros. Pero cuando los astrónomos quisieron representar con más precisión el movimiento de retrogradación de los planetas fue necesario modificar el modelo de Eudoxo. El discípulo de Aristóteles, Calipo de Cicico (370-310), añadió al sistema de Eudoxo, otras veintidós esferas que giraban en sentido contrario. Combinando los movimientos de las esferas se lograba representar el movimiento, irregular de los planetas, que ya no era circular y uniforme, como el de las estrellas. Precisamente fue el modelo de Calipo el que adoptó Aristóteles como estructura del cosmos. Evidentemente Eudoxo y Calipo describieron la estructura.
Pero, para conocer racionalmente la dinámica de ese cosmos había que conocer las causas de originaban esos movimientos, para ello supuso que la causa primera del movimiento cósmico estaba fuera de ese cosmos y que procedía de un motor inmóvil que actuaba directamente sobre la esfera más exterior, que era la esfera de las estrellas fijas. Las demás esferas cristalinas eran movidas por una serie de motores a los que el motor inmóvil transmitía movimiento. El movimiento circular de las esferas llegaba distorsionado, dañado y con irregularidades al mundo sublunar.
El mundo sublunar, era la región del cosmos situada dentro de la esfera de la Luna (sin incluirla), es decir, era la región terrestre, nuestro mundo. Lo que caracterizaba a esta región era el cambio. En esta esta parte del Cosmos, próxima al centro y más alejada del orden perfecto de las estrellas fijas y del motor inmóvil, tenía un comportamiento aparentemente caótico: había erupciones, se desataban tormentas, se padecían inundaciones, los seres vivos nacían y morían, también modificaban su tamaño, su peso, sus colores; los cuerpos chocaban entre sí y cambiaban de lugar o alteraban alguna otra cualidad. En ese mundo no había regularidades fácilmente observables como las que existían en el mundo supralunar. Era un mundo movedizo, cambiante y heterogéneo, sometido a la generación y a la corrupción, es decir, al cambio y estaba formado por los cuatro elementos tierra, agua, aire y fuego.
El mundo supralunar tenía un movimiento perfecto era la modelación realizada por Eudoxo de una idea platónica. Aristóteles pensó el mundo supralunar debía estar fabricado de un elemento diferente de los cuatro elementos del mundo sublunar, al que llamó éter, un elemento sutil e incorruptible, que solamente estaba sometido a un tipo de cambio, el movimiento circular; en clara oposición a los cuatro elementos (tierra, agua, aire, fuego) de los que estaba formado el mundo sublunar.
Estas disquisiciones Aristóteles las tiene repartidas entre muchas de sus obras físicas y algunos autores han hecho notar la evolución de su pensamiento. De acuerdo con la reconstrucción de la obra de Aristóteles realizada por Andrónico de Rodas (78-47 a. C.), en su obra Sobre el cielo, escrita en el 350 a. C. Aristóteles consideraba que el movimiento circular de las esferas cristalinas se debía a que ese movimiento estaba en la naturaleza del éter, como estaba en la naturaleza del elemento tierra el movimiento de vertical hacia el centro de la Tierra, lo que constituía una explicación de la dinámica celeste cercana al mecanicismo. Sin embargo, en los libros VII y VIII de la Física, que son posteriores, introdujo el concepto de motor inmóvil, lo que le permitía al estagirita establecer una interpretación teleológica del cosmos, ya que con esa hipótesis podía argumentar que el motor inmóvil, además de causa eficiente, también podía considerarse causa final, bastaba suponer que las esferas celestes intermedias tuvieran una especie de alma que les permitiera tener una aspiración creciente de alcanzar la perfección del motor inmóvil y esa aspiración actuaría como causa final que movería el cosmos.
Sea como fuere, podemos concluir que el pensamiento aristotélico transformó la idea de un cosmos puramente geométrico, como era el de las esferas cristalinas, situado en el mundo de las ideas, en un universo mecánico cuando le añadió la idea de la transmisión del movimiento desde del motor inmóvil situado sobre la esfera de las estrellas fijas y convertirlo en universo teleológico y organicista cuando supuso que las esferas cristalinas estaban dotadas de alma; con esa última suposición asumió las tesis de Platon en el Timeo, donde el fundador de la Academia consideraba al universo como un ser vivo inteligente.
Con el sistema de las esferas se podía representar el movimiento de los planetas, del Sol y de las estrellas fijas, pero con él no se podía explicar las variaciones en la luminosidad de los planetas.
Por esta razón, astrónomo, matemático y geógrafo greco-egipcio de Alejandría, Claudio Ptolomeo (90-170) pensó que eso era debido a que la distancia de la Tierra a los planetas cambiaba, lo que significaba, dado que los planetas se movían en órbitas circulares la Tierra no ocupaba el centro. Por esta razón modificó el sistema del cosmos de Aristóteles, pero sin poner en entredicho los principios puestos por Platón y Aristóteles.
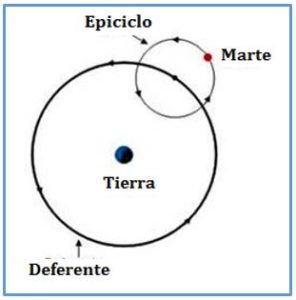
Ptolomeo concluyó que los planetas no estaban unidos a las esferas cristalinas centradas en la Tierra y, para no contradecir las hipótesis de los maestros, inventó un modelo complejo de composición de trayectorias. Los planetas describían órbitas circulares, llamadas epiciclos, alrededor de puntos que a su vez orbitaban en círculos alrededor de la Tierra, llamados deferentes. Por tanto, la órbita de todos los cuerpos celestes se podía explicar mediante la composición de dos movimientos circulares, el del epiciclo y el del centro del epiciclo, que describe una circunferencia, llamada deferente. Las trayectorias aparentes se podían explicar con esos ingenios geométricos y se aplicaron métodos de la geométricos y trigonométricos.
Con ese sofisticado modelo matemático, ajustando el tamaño de los epiciclos y el deferente, Ptolomeo consiguió que la composición de los movimientos circulares se ajustara a los datos observados desde la Tierra con bastante fidelidad y, además, con su modelo matemático podían justificar las variaciones en la luminosidad de los planetas, puesto que la distancia de estos a la Tierra era variable.
Ptolomeo modificó el modelo de esferas de Aristóteles para hacerlo más preciso, ajustado y acorde con las medidas de los astrónomos, pero el sistema del mundo y las ideas del modelo de Aristóteles se mantuvieron hasta el siglo XVI.
SALVAR LAS APARIENCIAS
El diccionario de la RAE da una ajustada definición de la locución verbal salvar las apariencias o salvar los fenómenos, que es la siguiente: Idear la explicación de un hecho observable sin certidumbre de la verdad. Lo que significa que salvar las apariencias es dar una explicación de refleje simplemente cómo se comporta un proceso ante nuestros ojos sin preocuparnos si nuestra explicación se ajusta a la evolución real del proceso que estudiemos. La frase se acuñó en los siglos XVI y XVII cuando se discutió sobre el significado que se debía dar a las diferentes teorías astronómicas o Sistemas del Mundo. En este análisis dejaremos a un lado las interferencias y las distorsiones que supuso la intolerancia religiosa en la relación entre la representación del mundo real por la ciencia realidad para hacer hincapié en el tema que nos ocupa que es la relación entre las matemáticas y la ciencia y más concretamente entre los movimientos de los cuerpos celestes y su representación geométrica.
La cosmología aristotélica y la astronomía griega estaban entrelazadas entre sí por la misma filosofía. Y ambas relacionadas con la religión hasta el siglo XVI. Pero, desde los comienzos hubo dos tendencias, dos corrientes de opinión sobre el sentido que se debía dar a las teorías astronómicas y, más concretamente, al significado de los modelos geométricos que se utilizaban, sobre todo desde Hiparco y Ptolomeo, para explicar y predecir el movimiento de los planetas en el cielo.
La cuestión de salvar las apariencias procede de una exigencia apriorística de Platón, que, inspirado en el armonioso y permanente e inmutable movimiento de los astros alrededor de la Tierra, el cual era semejante a las formas perfectas de su Mundo de la Ideas y siguiendo la tradición pitagórica, les pedía a los astrónomos que buscaran hipótesis que estuvieran de acuerdo con los fenómenos que pudieran salvar las apariencias. La exigencia era que cualquier cuerpo que se pudiera aparecer en el cielo debía llevar un movimiento circular, que era la forma de movimiento más perfecta, además, el movimiento del cuerpo celeste debía tener velocidad constante.
Heráclides de Ponto (388-315) discípulo de platón y coetáneo de Eudoxo y conocedor de su sistema de esferas cristalinas, probó que los movimientos de Venus y Mercurio podían ser descritos correctamente si, en lugar de considerar que los dos planetas giraban en torno a la Tierra, se suponía que ambos giraban alrededor del Sol y éste alrededor de la Tierra. Lo que suponía otra representación del Cosmos no tan compacta, pero también plausible. Dos siglos después Hiparco de Nicea (190-120 a.C.) demostró que la marcha del Sol alrededor de la Tierra se podía representar de dos formas equivalentes una siguiendo una circunferencia excéntrica alrededor de la Tierra, cuyo centro no estuviera en ella y otra mediante un epiciclo y un deferente.
Muchos astrónomos griegos tomaron las diferentes formas como modos válidos de resolver el problema planteado por Platón. Los astros se movían en órbitas circulares con lo que se cumplía con la exigencia de Platón y con cualquiera se salvaban las apariencias. Se obtenían los mismos resultados para determinar la efeméride de un astro. Por ejemplo, cualquiera de las representaciones proporcionaba al astrónomo, el mismo azimut, la misma altura y el mismo tiempo de aparición de un astro sobre el horizonte. Pero esto daba lugar a una pregunta: si distintas representaciones daban el mismo resultado¿Cuál era el verdadero movimiento de los planetas en el cielo?
Estas preguntas sobre las teorías astronómicas dieron lugar a dos tendencias sobre realidad de las teorías astronómicas. La primera la de los astrónomos, más matemáticos que físicos, que llamaremos tendencia formalista (tengamos en cuenta que la física de la época era la física de las cuatro causas) que se decantaba por que todas serían igualmente válidas y la segunda, propia de los físicos, que pensaban que debía haber alguna que se ajustara a la realidad de los cielos y que podría denominarse cosmológica, quele intersaba conocer lo que sucedía realmente en el universo.
Esta preocupación metodológica apareció reflejada, por vez primera en el astrónomo y matemático griego Gémino de Rodas (110-40 a.C.) autor de Isagoge, o Introducción a los fenómenos, obra que escribió para enseñar Astronomía. Dividió las matemáticas en dos bloque Mental y Observable, En la primera categoría colocó a la Geometría y a la Aritmética. En la segunda, a la Mecánica, a la Astronomía, a la Óptica y a la Geodesia. Géminio enseñaba, por ejemplo, que la esfera de las estrellas fijas, era solamente un modelo geométrico útil, ya que las estrellas estaban en realidad a distancias variables de la Tierra y no pegadas a una superficie esférica.
La tendencia formalista y la cosmológica se enfrentaron cuando en el siglo XVI apareció el libro de N. Copérnico (1473-1543), Sobre las revoluciones de los cuerpos celestes (1543), que fue publicado con un prólogo del editor de la obra y teólogo protestante A. Osiander (1498-1552) en el que afirmaba que el contenido del libro no era más que una hipótesis matemática útil para calcular los movimientos celestes. A esta forma de interpretar uno de los libros más relevantes de la revolución científica, se opusieron el propio Copérnico, su discípulo Rethico, J. Kepler (1571-1630) y Galileo (1564-1642), que entendieron la obra como un intento de describir y explicar la realidad y no como un simple recurso geométrico para salvar las apariencias.
De estas consideraciones surgieron diferentes interpretaciones de las teorías científicas en general: la instrumentalista y la realista. G. Berkeley (1685-1753), igual que el físico austriaco E. Mach (1838 -1916) que defendieron un claro instrumentalismo de las teorías que basta con que sean útiles sin necesidad de que sean verdaderas. Frente al instrumentalismo se oponía el realismo, que apoyaba que las teorías científicas debían ser aproximaciones verdaderas la realidad, postura heredera de la antigua tradición física aristotélica.
Víctor Ar
