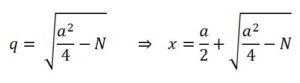En el año 1545, G. Cardano (1501-1576) publicó Ars Magna o las Reglas del Álgebra, la obra marcó un hito en la historia del Álgebra Renacentista, pues en ella aparecieron las fórmulas de resolución por radicales de las ecuaciones algebraicas de segundo, tercer y cuarto grado. Sin entrar en la polémica sobre la autoría del descubrimiento de la fórmula de resolución la ecuación de tercer grado entre Cardano y N. Tartaglia (1500-1557), se puede asegurar que Ars Magna fue una obra clave en el desarrollo de la Matemática porque, aunque el descubrimiento de las fórmulas de resolución de las ecuaciones de tercer y cuarto tenían en el momento escasas aplicaciones prácticas, el libro tuvo la virtud de estimular el desarrollo del álgebra, con el descubrimiento de los números complejos y de abrir la línea de trabajo que desembocaría una nueva visión del Álgebra y de las matemáticas a través de la teoría de grupos y el álgebra abstracta.
Ars Magna (1545) forma parte de una serie obras fundamentales que se publicaron en la década de los años cuarenta del siglo XVI: De revolutionibus Orbium Coelestiun (1543) de N. Copérnico (1473-1543), que supuso, en Astronomía, el cambio del Sistema Geocéntrico al Sistema Heliocéntrico y De humani corporis fabrica (1543) de A. Vesalio (1514-1564), el cual, con esta obra, se convirtió en el padre de la Anatomía Científica moderna en un momento en el que la Iglesia prohibía la disección de cuerpos y no era fácil estudiar anatomía.
Pero, aunque estemos hablando de obras cumbres de la ciencia, que han supuesto el origen de un período y han marcado la pauta de la evolución posterior, precisamente, el propio proceso evolutivo de cada una de ellas ha mostrado algunas limitaciones que el propio desarrollo del nuevo paradigma ha hecho matizar: Copérnico consideraba que las órbitas de los astros eran circulares (modificadas con epiciclos y deferentes..) y no elípticas, Vesalio, aunque descubrió que las arterias salían del corazón y no del hígado como afirmaba Galeno, tampoco conocía correctamente la circulación de la sangre. En este sentido podemos afirmar que Cardano no consideraba más que números positivos que representaban las magnitudes de la Geometría de Euclides y que, por lo tanto, los coeficientes de las ecuaciones debían ser debían ser números positivos y que las soluciones negativas carecían de sentido (Descartes aún las llamaba falsas en su Geometría (1639)) y que, además, no tenían sentido físico las raíces de números negativos, por esta razón distinguía tres tipos de ecuaciones de segundo grado.
Los tres tipos los designaba con Squeaxno, Noesquax y Axesquno. Que eran una forma del álgebra sincopada para designar el tipo de ecuación ya que las tres palabras están formadas por las cuatro abreviaturas: Squ (cuadrado), e (igual), ax (coeficiente de la primera potencia) y no (constante o número). Las abreviaturas se ordenaban de una forma u otra para indicar el tipo de ecuación, como sigue:
Primero: Squeaxno: (cuadrado (Squ), igual a (e) primera potencia (ax) y constante (no)):
x2 = ax +N
Cardano daba la siguiente regla de resolución: Suma el cuadrado de la mitad del coeficiente de la primera potencia con la constante de la ecuación y calcula la raíz cuadrada del total. A esto se le suma la mitad delcoeficiente de la primera potencia y la suma da el valor de x.
Segundo: Noesquax: (constante (No) igual a (e) cuadrado (squ), primera potencia (ax) )
N = x2 + ax
Cardano daba la siguiente regla de resolución: Suma el cuadrado de la mitad del coeficiente de la primera potencia con la constante de la ecuación y calcula la raíz cuadrada del total. A esto se le resta la mitad del coeficiente de la primera potencia y el resultado es el valor de x.
Tercero: Axesquno: (primera potencia (ax) igual a (e) cuadrado (squ) y constante (No) )
ax = x2 + N
Cardano daba la siguiente regla de resolución: Al cuadrado de la mitad del coeficiente de la primera potencia se le resta la constante de la ecuación y calcula la raíz cuadrada del total. El resultado se le resta a la mitad del coeficiente de la primera potencia o se le suma y el resultado es el valor de x.
Estas reglas de resolución, que Cardano las expresaba en la forma que se ha denominado Algebra Retórica, las dedujo a partir de consideraciones geométricas sobre la descomposición del cuadrado y esta deducción que se expresa de forma más actualizada a continuación:
Caso 1: Resolución del caso Squeaxno: x2 = ax + N (1)
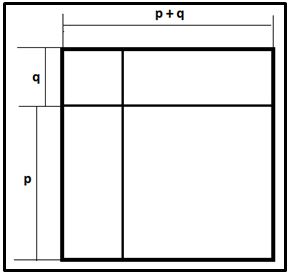
Dividimos el lado del cuadrado en dos partes p y q. El área del cuadrado de lado p+q será la suma de las áreas de dos rectángulos q(p + q) más la de otro cuadrado de lado p menos la de otro de lado q:
(p + q)2 = 2·q(p + q) – q2 + p2
Haciendo en esta igualdad p + q = x, queda x2 = 2qx – q2 + p2
e igualando coeficientes con (1) da lugar al sistema de ecuaciones:
2q = a p2 – q2 = N
De donde q = a/2 , y, por tanto:
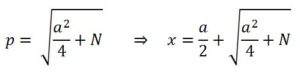
Caso 2– Resolución del caso Noesquax: x2 + ax = N (2)
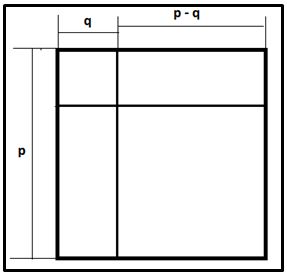
Dividimos un cuadrado de lado p cuadrado en dos partes: q y p-q. El área del cuadrado de lado p–q más las áreas de los dos rectángulos q(p – q) es igual a la diferencia del área del cuadrado de lado p menos la del cuadrado de lado q. Es decir:
(p – q)2 +2·q(p – q) = p2 – q2
Haciendo p – q = x, e igualando coeficientes con (2) da lugar al sistema de ecuaciones:
2q = a p2 – q2 = N
De donde q = a/2 y

Caso 3: Resolución del caso Axesquno: x2 + N = ax (3)
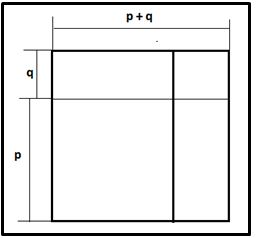
Dividimos el lado del cuadrado en dos partes p y q. El área del cuadrado de lado p+q más el área del cuadrado de lado q igual al área del cuadrado de lado p más las áreas de dos rectángulos q(p+q). Es decir: (p + q)2 + p2 = q2 + 2·p(p + q), que los podemos escribir en la forma:
(p + q)2 + (p2 – q2) = 2·p(p + q)
Haciendo p + q = x e igualando coeficientes con (3) da lugar al sistema de ecuaciones:
2p = a p2 – q2 = N
De donde p = a/2 y, por tanto: