La historia remonta los orígenes del Algebra hasta la época de Diofanto de Alejandría (siglo III), encuentra claros antecedentes en las proposiciones 5 y 6 del Libro II de los Elementos de Euclides (hacia el 300 a. de C.) en la parte que se ha denominado Algebra Geométrica y se observan antecedentes del Algebra en las cuestiones matemáticas encontradas en las tablillas de arcilla de la antigua Babilonia (2000-1600 a.C.). Los historiadores ven en esas manifestaciones un progreso, largo, incesante y disperso de antecedentes claros en el establecimiento del lenguaje algebraico, que acabaría por dominar toda la Matemática.
En este escrito me centraré en el desarrollo del Álgebra a partir de la aparición en occidente de las cifras indo-arábigas y del sistema de numeración decimal, por ser la parte final de la historia en la que los algoritmos, pero, sobre todo, las notaciones de la aritmética pasan a enriquecer las fórmulas del Álgebra y ésta se convierte en un lenguaje simbólico coherente en el que se podían expresar y resolver problemas reales.
Estas cifras y el sistema de numeración posicional eran utilizados por los matemáticos hindúes, los cuales, entre los siglos V y XII, elaboraron un modo de abordar los problemas matemáticos basado en las reglas aritméticas de cálculo. Realizaban operaciones con números negativos, utilizaron la regla de los signos, introdujeron el cero como cifra y profundizaron en la elaboraron de las reglas para resolver ecuaciones lineales y cuadráticas. Evidentemente, este modo de trabajar las matemáticas apuntaba hacia una nueva línea diferente de la orientación, casi exclusivamente geométrica, de la matemática griega.
A partir del siglo VII, el sistema de numeración hindú se extendió por los países del mar Mediterráneo debido a los contactos comerciales del recién nacido Imperio Árabe con la India. La expansión árabe desde la India y, por todo el Mediterráneo, hasta España hizo que los árabes adoptaran el sistema de numeración hindú, con sus reglas operativas y la representación de sus diez cifras y fueran el hilo conductor de la difusión del sistema de numeración hindú en Occidente.
La Aritmética y resolución de ecuaciones de las matemáticas hindúes fue recogida por el mundo islámico, que también había conocido la Geometría Griega en su expansión por Alejandría. Y sabios de talla como Al-Khawarizmi (780-850) matemático de la Casa se la Sabiduría de Bagdad realizaron una labor de fusión entre ambas tendencias de la matemática (griega e hindú) de una forma de pedagógica para facilitar el estudio de la matemática.
Los árabes pretendían romper con aquel precepto que se había establecido desde los tiempo de Alejandro Magno (356-323 a. de C.) cuando éste le preguntó a su tutor y maestro, el matemático Menecmo (375-320 a. de C.), si no habría un atajo o camino más fácil para aprender la Geometría, a lo que el matemático le contestó: Señor, para viajar por tu gran imperio hay calzadas reales y sendas para caminantes, pero en Geometría hay un solo camino para todos.
Sin embargo Al-Khawarizmi decía:
“Quiero dedicarme a hacer fácil el estudio de la matemática a todas las personas. No quiero hacer una ciencia que no se aplique a los problemas de la vida diaria y no los beneficie”
Al-Khawarizmi publicó un libro transcendental titulado Kitab al-jebr wal-muqabalah. Del término al-jabr, que significa reducción, se deriva la palabra álgebra y del nombre del autor el término algoritmo. En el libro se daban las reglas para realizar la transposición de términos y posterior simplificación de términos semejantes en una ecuación. Una posible traducción del título sería El libro de la restauración e igualación y contenía algunos métodos para resolver ecuaciones primer y segundo grado y, además, abordaba algunos problemas de Geometría.
La obra Kitab al-jebr wal-muqabalah fue traducida al latín por primera vez por Adelardo de Bath (1080-1152) hacia el año 1120 en la Escuela de Traductores de Toledo y tuvo mucha influencia en las matemáticas de la época. Al-Khawarizmi utilizaba para designar la incógnita la palabra árabe shay que en las traducciones latinas se tradujo por res y en italiano y en español por cosa.
Debemos tener en cuenta que las cifras arábigas fueron menciones por primera vez en la literatura occidental se encuentran en el Codex Vigilanus del año 976. Gerberto de Aurillac (945-1003) las llevó para Francia desde la España árabe en hacia 980 y, que luego, cuando fue nombrado Papa con el nombre de Silvestre II, y desde su privilegiada posición contribuyó a difundir el conocimiento del sistema de numeración en Europa sobre todo en los Monasterios, en las Universidades y entre todos los que hablaban latín
Por otra parte, comerciantes como Leonardo de Pisa (1170-1250), alias Fibonacci (filio Bonacci, hijo de Bonacci), escribieron Aritméticas para su uso en los negocios. Fibonacci era hijo del representante de los mercaderes de Pisa que comerciaban en el norte de África. Por eso estudió Algebra y el sistema de numeración de los árabes en una Escuela de Contabilidad de Bugia (Argelia) y así lo cuenta en el Liber Abaci (1202):
Cuando mi padre, que había sido nombrado por su país como notario público de la aduana en Bugia en representación de los mercaderes pisanos que iban allí, me llevó con él siendo yo todavía un niño, y teniendo un ojo para lo útil y las conveniencias futuras, quiso que permaneciera allí y recibiera instrucción en la escuela de contabilidad. Cuando fui introducido al arte de los nueve símbolos de los hindúes por medio de una muy buena enseñanza, el conocimiento del arte muy rápidamente me complació sobre todo lo demás y logré entenderlo…
Las aritméticas para comerciantes gozaron de gran predicamento, de hecho se publicaron muchas en los siglos XIII, XIV y XV y contribuyeron a fomentar el manejo de los números arábigos y a su difusión en lengua romance.
En este contexto J. Sacrobosco (1195-1256), profesor de Astronomía de la Universidad de Paris. Explicaba en sus clases la aritmética de los árabes y escribió un tratado titulado Algorismo en el que enseñaba cómo realizar sumas restas, multiplicaciones y divisiones, raíces cuadradas y cúbicas con los números arábicos. Por otra parte en Génova, en Venecia, en Pisa y en otras muchas ciudades aparecieron unos manuales específicos de aritmética para mercaderes, llamados Manuales de Ábaco, que se explicaban en las Escuelas de Ábaco y garantizaban la instrucción que necesitaban los hombres de negocios.
En estas obras se generalizaban los métodos indoarábigos y también se resolvían problemas que implicaban ecuaciones lineales, de segundo grado y, algunas de tercero.
Prueba de la importancia que tuvieron estas Aritméticas es que, tras la invención de la imprenta a mediados del siglo XV, la Aritmética de Treviso de 1478, escrita para comerciantes fue la primera obra matemática impresa, y se imprimió cuatro años antes que los Elementos de Euclides, obra cumbre de la matemática griega.
Entre las Aritméticas más completas e influyentes se pueden destacar Triparty e N. Chuquet (1440-1500) y Summa de Aritmética (1494) de Luca Pacioli (1445-1517), en ellas (y en casi todas) se resolvían problemas en los que había que hallar la incógnita que cumplía una serie de condiciones, es decir que implicaban la resolución de ecuaciones y se realizaban abreviaturas precursoras de un cálculo con letras semejante al que se hacía en aritmética.
Las recetas para resolver ecuaciones expresaban de forma retórica, es decir, indicando los pasos que se debían hacer para resolverlas en la lenguas vernáculas así, por ejemplo en Ars Magna (1545) de G. Cardano (1501-1576) de la ecuación x cubus p latus aequal q [ x3 + px = q] y explica la regla aplicándola la ecuación x3 + 6x = 20
Eleve al cubo un tercio del número de lados (p) [dará 8] adicione a esto, el cuadrado de la mitad de la constante de la ecuación (q) será 100, y tome la raíz cuadrada de todo. Pondrá esto dos veces, y a una de las dos adicione una mitad del número del que ha encontrado el cuadrad (p/2) y del otro, usted sustrae una mitad del mismo (p/2). Usted tendrá entonces un binomio √108+10 y esto es epítome √108-10. Entonces substrae la raíz cúbica de la epítome de la raíz cúbica del binomio, el residuo es el lado buscado.
En lugar de escribir:
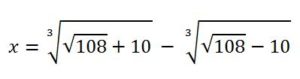
Esta situación indica que hubo una serie de etapas orientadas a la creación de un cálculo literal y lograr con ello un avance en varios sentidos, el primero era ahorrar esfuerzos al unificar con un mismo lenguaje todas las abreviaturas, signos y reglas utilizados por los diferentes matemáticos para la resolución de problemas numéricos y, lo que no es menos importante, con el lenguaje algebraico se podía, además, de obtener el resultado final, poder seguir el razonamiento y la influencia de los datos para conseguir el resultado.,
En reumen, se estaba fraguando con la confluencia de los métodos de la aritmética y la inspiración del rigor de la geometría un nuevo lenguaje, un idioma para resolver problemas numéricos. En el siglo XVI se realizó una lenta sustitución del cálculo con el ábaco por el cálculo las reglas ordinarias del cálculo con las cifras indoarábigas y, a partir de su adopción la Aritmética difuncida con una notación potente creada por fundamentalmente por los aritméticos alemanes a través de la Enciclopedia Margarita philosophica de Gregor Reisch (1503), surgieron algebras como la de Adam Riese (1492-1559) que escribió Die Coss o la M. Stifel (1487-1567) con su Arithmetica integra (1544) en la que se trataban por primera vez el cálculo con potencias de exponente racional.
A finales del siglo XVI, al álgebra, se encargaba de la resolución de ecuaciones y en suma de calcular con símbolos. Viète (1540-1603) en su obra In Artem Analyticem Isagoge (1591) denominó al Álgebra Aritmética Speciosa, para distinguirla de la Aritmética Numerosa. A comienzos del siglo XVII muchos vieron las ventajas de trabajar con el algebra. Descartes (1596-1650) aplicó directamente el cálculo literal a la a la Geometría y fue seguramente la Géométríe de Descartes, a través de la traducción latina de F. Van Schhoten (1615-1660), la obra más influyó en la difusión de la notación y el lenguaje algebraicos. En ella se difundió masivamente la notación literal cartesiana hasta el punto, que su Geometría, heredera de la Aritmética Speciosa de Vieta y de los aritméticos alemanes, fue la obra que estudiaron I. Newton (1643-1727) y G. Leibniz (1646-1716).
Wallis (1616 – 1703) y Newton llamaron al Algebra Aritmética Universal. Wallis escribió en en 1657 Mathesis universalis sive Arithmeticorum opus integrum (1657) e I. Newton en 1707 publicó Arithmetica universalis: sive de compositione et resolutione arithmetica) y ambos afirmaban que la Aritmética Universal permitía ver complejas relaciones matemáticas.
No todo el mundo aceptó el Algebra como rama de las matemáticas Th. Hobbes (1588-1679) en su obra Examinatio et emendatio mathematicae hodiernae qualis explicatur in libris Johannis Wallisii (1660) [El examen y la mejora en la calidad de la matemática actual que se explica en el libro de Wallis] despreciaba al Algebra diciendo que no era ciencia sino un razonamiento simbólico. Igualmente, I. Barrow (1558-1679), maestro de Newton, también consideraba que el Álgebra era una rama de la lógica. Quizás por estas consideraciones Newton no escribió los Principia (1687) en el lenguaje del Álgebra y lo hizo basándose en la Geometría de Euclides. G.P. Roverbal (1602-1665) decía que había utilizado y = xm para realizar cuadraturas.
El álgebra es heredera directa de la aritmética indoarábiga con un largo periodo gestación semejante al que se realiza para elaborar cualquier lenguaje e includo humano lenguaje.