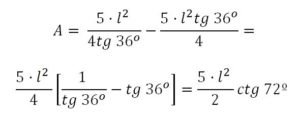La estrella de cinco puntas, también llamada Estrella Pitagórica, Pentagrama o Pentalfa, está estrechamente relacionada con las proporciones de la belleza y con el número áureo. Está formada por las cinco diagonales de un pentágono regular y tiene varias propiedades geométricas: puede ser paseada entera sin recorrer dos veces el mismo lado, está formada por cinco alfas mayúsculas. Las relaciones profundas encerradas en la estrella y relacionadas con la armonía y la belleza fascinaron a los Pitagóricos. Algunas de esas curiosidades de la estrella se muestran a continuación en las relaciones fundamentales en el pentágono regular entre las siguientes lineas: Diagonal , lado, apotema y radio del pentágono y lado de la estrella (d, lp , ap, rp, , le ).
Proposición 1.- Las diagonales trazadas desde un vértice del pentágono regular trisecan el ángulo interior del mismo.
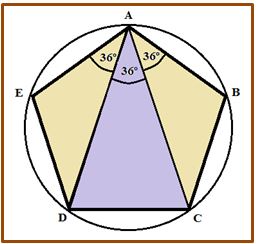
Demostración: Los cinco arcos en que se divide la circunferencia: AB, BC, CD, DE, EA son iguales y miden 72º . Por otra parte, el ángulo interior EAB del pentágono mide 108º y :
Ang(EAB) = Ang(EAD) + Ang(DAC) + Ang(CAB)
Pero Ang(EAD) = Ang(DAC) = Ang(CAB) = 36º,
por ser ángulos interiores en una circunferencia que abarcan arcos de 72º y los ángulos interiores miden la mitad del arco que abarcan sus lados. Y, evidentemente, 36º · 3 = 108º
En consecuencia, dado que el pentágono regular es un polígono construible con regla y compás, el ángulo de 108º se puede trisecar con regla y compás.
Proposición 2.- La razón entre la diagonal y el lado del pentágono es el número áureo (𝜙).
Demostración: Trivialmente se observa que los triángulos isósceles ACD y CBD’ son semejantes por lo que:
![]()
observemos que AC = d es la diagonal y que DC = CD’= l es igual al lado. Por lo tanto, la relación (1) la podemos escribir:
![]()
⇒ d2 – dl – l2 = 0 ⇒ (tomando la solución positiva)
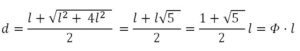
Consecuencia 1.- El cociente entre la diagonal (d) y el lado (l) del pentágono es 𝜙.
Consecuencia 2.- La diferencia entre la diagonal (d) y el lado (l) del pentágono, d – l = le, es el lado de la estrella de cinco puntas (le = d – l)
Consecuencia 3.- La razón entre el lado del pentágono (l) y el lado de la estrella, (d – l), es 𝜙.
Proposición 3.- La expresión trigonométrica de 𝜙 es 𝜙 = 2· cos36º
Demostración: Por la consecuencia 1 ⇒ d = l 𝜙 · .
También se cumple por las consecuencias 2 y 3 que
l = (d – l)·𝜙 = ,le·𝜙 = l / le
Por otra parte en el triángulo A’CD se deduce que:
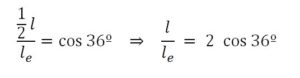
Por la consecuencia 3 se sigue que 𝜙 = 2 cos 36º
Proposición 4 .- La razón entre la apotema y el radio del pentágono regular es la mitad del número áureo (𝜙/2).
Demostración: de la figura anterior se deduce que ap = rp· cos 36º ⇒
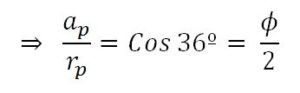
Proposición 5.- Longitud del perímetro de la estrella pitagórica es 10 l / 𝜙
Demostración: La Estrella Pitagórica tiene diez lados y cada uno mide (d – l):
Perímetro = 10(d – l )= (por la consecuencia 3) = 10 l/ 𝜙
Cálculo del área de la Estrella en función del lado del pentágono
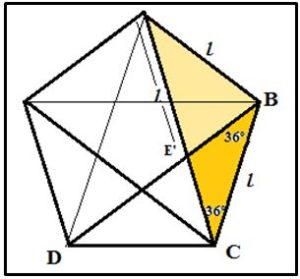
Area de la Estrella = Area del pentágono – 5 Area del triángulo BCE’. Area del triángulo :
![]()
Areal del pentágono:
La Apotema será

El área de la estrella será: