La física de Newton transformó las Leyes de Dinámica Galileana y los principios mecánicos cartesianos en una formulación matemática en la que estaban incluidas las causas del movimiento.
El Principio de Inercia establecía que todo cuerpo permanecía en su estado de movimiento rectilíneo y uniforme, siempre que no actuara sobre él una fuerza. Este Principio, que Newton adoptó como primera ley de su Mecánica, le permitió relacionar las fuerzas con los cambios de velocidad, esto es, con las aceleraciones. Las leyes fundamentales de la Mecánica de Newton estaban firmemente ligadas al movimiento físico.
Las fuerzas podían medirse con dinamómetros y las aceleraciones podían calcularse, ya que el cambio de velocidad era medible y cuantificable de las formas más diversas (Galileo había medido la g de la gravitación haciendo caer bolas por planos inclinados) y la Mecánica de Newton había llenado el espacio de fuerzas atractivas en todas las direcciones y entre todos los cuerpos existentes. Como no había ningún principio interno o tendencia que impulsara a los objetos físicos o indicara un comportamiento particular de los mismos, los resultados se obtenían a partir del equilibrio de fuerzas y de momentos. Esta forma newtoniana de estudiar la naturaleza y el movimiento se llama Mecánica Vectorial, ya que todas las que variables con las que se trabajan se expresan mediante vectores.
Escribir ecuaciones del movimiento en forma vectorial, a veces, era difícil, y, en ocasiones, aunque hubiera sido posible escribir dichas ecuaciones, las soluciones eran muy difíciles de obtener.
Algunos físicos, para facilitar los complicados cálculos de la Mecánica Vectorial, abordaron una nueva forma de estudiar a la naturaleza usando el Principio de la Conservación de la Energía Mecánica, que dice que, en ausencia de rozamiento y sin mediación de ningún trabajo externo, la suma de las energías cinética y potencial permanece constante.
Debemos recordar que lo que conocemos como Ley de Conservación de la Energía es un concepto más amplio, que incluye la conservación de diferentes tipos de energía (eléctrica, térmica, gravitacional, elástica, etc..). Lagrange se refería exclusivamente al principio de la conservación de la energía mecánica.
El Principio de Conservación de la Energía Mecánica tiene su antecedente en el principio de conservación de la fuerza vivas, que fue desarrollado por G. Leibniz (1646-1716) y D. Bernoulli (1700-1782). Leibniz definió fuerza viva como una magnitud proporciona a mv² (E α mv²) que describe la energía cinética como la fuerza viva o vis viva. W. Gravesande (1688-1742) realizó un experimento que relacionaba la energía cinética (vis viva) con la energía potencial: Dejó caer dos pesos puntiagudos sobre un bloque de arcilla desde diferentes alturas y observó que la profundidad de penetración era proporcional al cuadrado de la velocidad del impacto, lo que relacionaba la energía potencial (gravitatoria) de un cuerpo, con la energía cinética.
J.L. Lagrange (1736-1813) aportó una regla diferente, un principio cualitativo que se expresaba como un principio de mínimo, con el que se obtenían los mismos resultados que con las leyes de la Mecánica de Newton. El principio básico que formuló fue que la naturaleza actuaba siempre minimizando la acción. Pero ¿Qué es una acción? ¿Por qué tiene que ser mínima? ¿De dónde procede esa inspiración?
La inspiración arranca del principio de mínimo que estableció P. Fermat (1607-1665) para la propagación de la luz, que afirma que la trayectoria de la luz, al propagarse de un punto a otro, es tal que emplea un tiempo mínimo en recorrerla.
La misma idea expuso P.L. Maupertuis (1698-1759) en las Memorias de la Academia de ciencias en su trabajo, Concordancia de diferentes leyes de la naturaleza que hasta ahora parecían incompatibles (1744).
…Meditando profundamente sobre esta materia, he pensado que la luz, cuando pasa de un medio a otro, abandonando la ruta más corta, que es la línea recta, podría también no tomar el camino de tiempo mínimo. En efecto, ¿qué preferencia habría de haber aquí del tiempo sobre el espacio? La luz, no pudiendo recorrer a la vez el camino más corto y tomar el de tiempo mínimo, ¿por qué tendría que elegir uno prefiriéndolo al otro? Tampoco seguiría ninguno de los dos, tomaría el camino que tuviera una ventaja más real: que sería el camino para el cual la cantidad de acción es la menor…
Leonard Euler (1707-1783) se ocupó de problemas como los siguientes:
Determinar, entre todas las trayectorias posibles el camino más corto que une los puntos A(x1,y1) y B(x2,y2). Es decir, la curva y(x) que hace que la longitud de ella, L, entre A y B entre sea mínima:
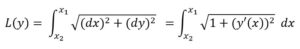
Para que esa L(y) sea mínima y(x) debe ser una recta y(x) = mx + b
El problema de la braquistocrona: Es la curva y(x) que hace que una partícula, sometida a la acción de la gravedad, emplee un tiempo T(y) mínimo en recorrerla entre dos puntos A(x1, y1) y B(x2, y2)
Es la cicloide de ecuaciones paramétricas: x = R(α – sen α) , y = R(1 – cos α).
Euler se ocupó de problemas más generales el cálculo de variaciones Dada una función (funcional) f(x, y(x), y(x’), tenemos que encontrar la curva y = y(x) que hace que la integral
tenga un valor mínimo.
Este cálculo se conoce como Cálculo de Variaciones y fue iniciado por L. Euler (1707-1783) en su trabajo Elementos del cálculo de variaciones (1733), aunque el Cálculo de Variaciones alcanzó mayor relevancia y protagonismo cuando J.L. Lagrange lo aplicó al estudio de la Mecánica. Este matemático en 1755, con diecinueve años, resolvió el Problema Isoperimétrico, o problema de Dido. y envió su demostración en una carta a Euler, que era considerado (y con razón) el matemático más importante del siglo XVIII. Euler se interesó por el método que había que había empleado que era el del Cálculo de Variaciones y estaba de acuerdo con el resultado, porque él mismo lo había hallado antes. Euler, con una generosidad fuera de la habitual, respondió a Lagrange elogiando el trabajo del joven matemático y no hizo mención de su descubrimiento anterior para quitar méritos a Lagrange.
En realidad, Lagrange no sólo había resuelto un problema clásico de las matemáticas, también había inventado un nuevo método para realizar los cálculos de la Mecánica Vectorial de Newton a partir de una función escalar. Lagrange definió una función escalar para cada sistema dinámico particular, que mediante el Cálculo de Variaciones permitía hallar las ecuaciones de movimiento del sistema. Si T es la energía cinética y V la potencial, entonces la lagrangiana es L = T – V. La ecuación de Lagrange correspondiente a la coordenada generalizada qi y su derivada q’i, (que pueden ser x(t) y x’(t))
L(x(t), x’(t)) = T – V = (1/2) m· (x’(t))2 – V(x(t))
Buscaremos una x(t) que haga mínimo S(x(t)), esa condición se cumple si:
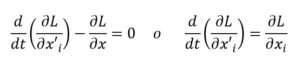Es una ecuación diferencial en x(t)
Con el cálculo Lagrange podía demostrar que las leyes de Newton de materia y movimiento, que se adaptaban al amplio principio de economía de la naturaleza. El principio ha conducido a los resultados y planteamientos, aún más fructíferos, de W. Hamilton (1805-1865), A. Einstein (1879-1955) y E. Noether (1882-1935).
Lagrange prescindió de las fuerzas que actuaban sobre las diferentes partes del sistema y, con la Lagrangiana, obtenía las ecuaciones diferenciales del movimiento, que permitía escribir las ecuaciones de forma generalizada de manera que formalmente eran iguales.
