
Las matemáticas están formadas por teorías profundas y bellas que nos han hecho comprender y explicar el mundo que nos rodea. Las teorías matemáticas, con sus teoremas penetrantes, brillantes y abstractos, han hecho avanzar las ciencias a niveles altísimos. Muchas teorías matemáticas han sido utilizadas para resolver problemas del mundo real y han ofrecido a las ciencias y, aún hoy siguen proporcionando, nuevas formas de representar y comprender racionalmente el mundo que nos rodea.
Además de los grandes teoremas, las matemáticas nos ofrecen una serie de resultados sorprendentes, pequeños y bellos logros, que se muestran como asombrosas coincidencias y parecen mostrarnos de forma cristalina la regularidad, la belleza y la armonía del pensamiento matemático, y nos remontan a la relación entre la geometría y la belleza de las ideas platónicas.
A continuación, mostraremos cuatro teoremas, que representan bellas propiedades geométricas, aunque tengan escasa trascendencia teórica. El primero es el teorema de Morley, claramente relacionado con uno de los tres problemas clásicos griegos, conocido como el Problema de la trisección del ángulo con regla y compás, aunque su origen es seguramente más antiguo, apareció claramente planteado en Grecia hacia el siglo IV a. de C.
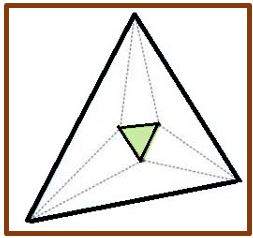
Después de demostrada la imposibilidad de ser resuelto con la exigencia de hacerlo con la regla y el compás, hacia 1900, el matemático F. Morley (1860-1937) descubrió un teorema que relaciona las trisectrices de los tres ángulos de un triángulo
Teorema de Morley.- Los tres puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera son los vértices de un triángulo equilátero.
Hoy en día, gran parte de la investigación de Morley parece tener una importancia poco convincente, pertenece al grupo de matemáticos problemistas y uno se siente tentado de considerar sus intereses en la materia como los de un aficionado talentoso, un artista que se deleita con las cosas pequeñas y hermosas, en lugar de elucubrar sobre los de un matemático profesional de primera linea. Sin embargo, sea cual sea el significado que uno elija otorgarles, a Morley se le debe dar crédito por plantearse tales preguntas y darles respuesta.
El segundo teorema que vamos destacar se conoce con dos nombres diferentes. Aunque lo dio a conocer el matemático italiano Lorenzo Mascheroni (1750-1800), se ha conocido, por una falsa atribución, como Teorema de Napoleón, ya que Mascheroni publicó el resultado en su obra Geometria del compasso (1797) y había dedicado el libro a Napoleón Bonaparte y, por error, se le adjudicó la autoría al Emperador.
En ese libro, Mascheroni demostró que cualquier construcción geométrica que pueda realizarse con regla y compás se puede hacer únicamente con compás. Este resultado lo había publicado en 1672 el matemático danés Georg Mohr (1640- 1697), no obstante, Mascheroni desconocía la publicación y hoy el resultado se conoce como Teorema de Mohr-Mascheroni.
El teorema de Mascheroni, publicado en la Geometria del compasso dice lo siguiente:
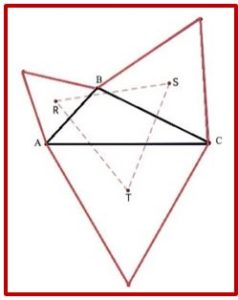
Teorema de Mascheroni: Si sobre los tres lados de un triángulo cualquiera ABC se construyen tres triángulos equiláteros exteriores (respectivamente, interiores), los centros de estos tres triángulos equiláteros forman un nuevo triángulo RST, que es equilátero, al que se denomina triángulo exterior (respectivamente, interior) de Napoleón. (Según se muestra en la figura)
El tercer teorema es el Teorema de Pascal o del Hexagrama Místico, que fue enunciado por el matemático francés Blaise Pascal (1623-1662). El Teorema es una generalización de un Teorema de Pappus de Alejandría (290–350), de hecho, el Teorema de Pappus correspondería al caso en el que el teorema de Pascal se formulara para una cónica degenerada formada por dos rectas.
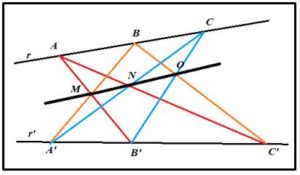
Teorema de Papus: Si r y r’ son dos rectas cualesquiera y y tomamos tres puntos sobre cada recta (A, B, C sobre r y A’, B’,C’ sobre r’), si trazamos los segmentos rectilíneos que unen los puntos de las rectas que tienen letras diferentes (no dibujamos las rectas AA’, BB’, CC’). Los puntos: M que determina AB’ con BA’, N determinado por AC’ con CA’, y O, intersección de BC’ con CB’ están alineados.
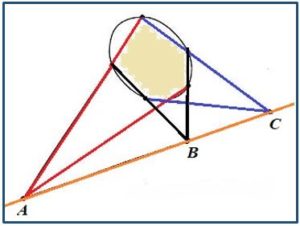
Teorema de Pascal. Los puntos de intersección de las prolongaciones de lados opuestos de un hexágono inscrito en una circunferencia (elipse, o cónica en general) están alineados
No se conoce la demostración de Pascal ya que su escrito original se perdió. Pero G. Leibniz (1646-1716), alabó mucho el ingenio de la demostración del joven matemático. Hoy el teorema forma parte de la geometría proyectiva y se conocen muchas demostraciones.
Acabaremos con un curioso teorema conocido como el Teorema de la recta de L. Euler (1707.1783) que se verifica para un triángulo cualquiera, y dice simplemente:
Recta de Euler: El ortocentro, el baricentro, y el circuncentro de un triángulo cualquiera están alineados.
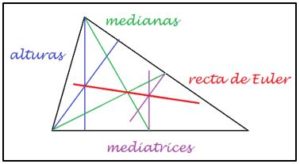
El ortocentro es el punto en el que se cortan las alturas del triángulo
El baricentro es el punto en el que se cortan las medianas de un triángulo
El circuncentro es el punto en el que se cortan las mediatrices de los lados del triángul

