PROBLEMA 1: Hallar los valores n para los que. (5n+ 26) /(2n+3) es un número entero
SOLUCIÓN : Observemos que:
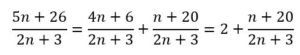Para que:
Se debe cumplir que 2n + 3 ≤ n + 20 ⇒ n ≤ 17. Y entre todas las fracciones factibles:
21/5, 22/7, 23/10, 24/11, 25/13, 26/15,
27/17, 28/19, 29/21, 30/ 23, 31/25, 32/27,
33/ 29, 34/31, 35/33, 36/35, 37/37
Solo es reducible 37/37, que se da cuando n =17
PROBLEMA 2: Hallar los valores de n para los que la expresión (28n3+56n+90) / (n2+2) toma valores naturales
SOLUCIÓN:
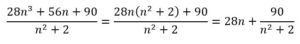
Es necesario que
sea entero para lo cual n2+2 debe ser divisor de 90.
Los divisores de 90 son 1, 2, 3, 5, 6, 9, 10,15,18, 30, 45, 90.
Por otra parte n2+2 ≤ 90 ⇒ n2 < 88 , por tanto como n2 será uno de los valores
1, 4, 9,16, 25, 36, 49, 64, 81
Y n2 + 2 será uno de los valores 3, 6, 11, 18, 27, 38, 51, 66, 83, pero, además, tiene que ser divisor de 90, lo valores de n2 + 2 serán 3, 6, 18 ⇒ valores factibles de n2 serán 1, 4, 16 y los de n= 1,2,4
Problema 3: ¿ Para qué valores de n la fracción
es irreducible?
Solución: Para que sea reducible debe existir d debe que divida sus dos términos, es decir a (4n + 5) y a (2n – 3). Utilizando la propiedad:
Si b, c y d son números enteros y d |b y d|c entonces d | mb + nc, siendo m y n dos enteros cualesquiera
En particular, d dividirá a a(4n + 5) – 2a(2n – 3) = 11a, siendo a un enteros cualquiera. Luego d debe ser 11 o múltiplo de 11.
Observamos que, para n = 7, 4n + 5 = 33, múltiplo de 11 y 2n -3 = 11, ambos múltiplos de 11 múltiplo de 11
Encontrado el primero, seguimos de 11 en 11
Para n = 18 4n + 5 = 77 y 2n -3 = 33 (divisibles por 11)
Para n = 29 4n + 5 = 121 y 2n -3 = 55 (divisibles por 11)
Para n = 40 4n + 5 = 165 y 2n -3 = 77 (divisibles por 11)
Para n = 51 4n + 5 = 209 y 2n -3 = 99 (divisibles por 11)
Para n = 62 4n + 5 = 253 y 2n -3 = 121 (divisibles por 11)
Para n = 73 4n + 5 = 297 y 2n -3 = 143 (divisibles por 11)
Para n = 84 4n + 5 = 341 y 2n -3 = 165 (divisibles por 11)
Para n = 95 4n + 5 = 385 y 2n -3 = 187 (divisibles por 11)
………………….
Luego la fracción es reducible para n = 7 +11k , para k = 0,1, 2…, Y será irreducible para los restantes
Problema 4: Encontrar para qué valores de n la fracción (5n + 6)/(4n+1) es irreducible
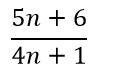
SOLUCIÓN: Si fuera reducible debería haber un número d que dividiera a:
(5n+6) y (4n + 1) para determinados valores de n y por la propiedad:
Si d |b y d|c entonces d | mb + nc
El número d dividirá 4a(5n + 6) – 5a(4n + 1) = 24a – 5a = 19a, luego podría ser d
será 19
Si n = 14 5n + 6 = 76 y 4n + 1 = 57 (divisible por 11)
Si n = 33 5n + 6 =171 y 4n + 1 = 136 (divisible por 11)
Si n = 52 5n + 6 = 266 y 4n + 1 = 209(divisible por 11)
……..
La fracción será irreducible para n = 14 +19k , para k = 0,1, 2.. irreducible los restantes valores de n
PROBLEMA 5: Probar que la fracción
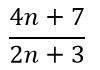es irreducible para todo valor de n.
SOLUCIÓN: Para que sea reducible debe existir un d que dividir a (4n + 7) y (2n + 3)
Utilizando la propiedad: Si b, c y d son números enteros y d |b y d|c entonces d | mb + nc, siendo m y n dos enteros cualesquiera
El supuesto número d también deberá dividir a a(4n + 7) – 2a(2n – 3) = 1a luego debe dividir a los múltiplos de 1, es decir, a todos los números naturales, lo que es absurdo, por tanto, no existe el d buscado y la fracción es irreducible para todo valor de n.
