
Si un bastón se rompe en tres trozos, ¿cuál es la probabilidad de que con esos tres trozos se pueda formar un triángulo?
Las condiciones para que tres segmentos rectilíneos a, b y c puedan formar un triángulo es que cada uno de ellos tiene que medir menos que la suma de los otros dos.
a < b + c b < a + c y c < a + b
Esta propiedad se conoce como Desigualdad Triangular
Al partirse un bastón de longitud un metro en tres trozos se podrá formar un triángulo si todos los trozos miden menos de medio metro, ya que, si alguno de los trozos midiera igual o más que medio metro, la suma de los otros dos trozos sería menor o igual que medio metro, y no se verificaría la Desigualdad Triangular.
Para calcular la probabilidad de que un bastón de longitud uno se rompa en tres trozos x, y, z se debe cumplir:
- Por ser trozos del bastón x, y, z deben ser positivos y cumplir la condición; x + y + z = 1.
- Para que los trozos x, y, z puedan formar triángulo deben cumplir la Desigualdad Triangular, que, aplicada al bastón, será: x < 0,5, y < 0,5, z < 0,5.
Solución 1:
En el espacio geométrico tridimensional un punto M de coordenadas (x, y, z) que cumpla que x + y + z = 1 pertenece al plano que tiene esa ecuación, que con las condiciones: x > 0, y > 0, z > 0, será la región de los puntos del plano cuyas coordendas son todas las medidas posibles de los trozos en que puede romper el bastón:

El plano x + y + z = 1 corta los ejes positivos en los puntos de
A(1, 0, 0) B(0, 1, 0) y C(0, 0, 1)
que son los vértices de un triángulo equilátero dentro del cual están todos los puntos cuyas coordenadas representan todas las medidas posibles en las que el bastón se puede dividir en tres partes.
Los puntos tales que sus tres coordenadas miden todas menos de 0,5 ( x < 0,5, y < 0,5, z < 0,5), forman la región que contiene todos los puntos con cuyas coordenadas se puede formar un triángulo y están dentro del triángulo amarillo de vértices P (0,5, 0,5, 0), Q (0, 0,5, 0,5), R ( 0,5, 0, 0,5), cuya área es la cuarta parte de la del triángulo ABC, por lo tanto:

Solución 2: Supongamos bastón de longitud un metro, representado por el intervalo (0,1). Tomemos en ese intervalo dos puntos P y Q que dividen al intervalo en tres partes

Supongamos OP = x y OQ = y y que x < y. Los torzos de cualquier fractura posble del bastón en tres trozos, que representamos en el intervalo (0,1) y debe complir las son:
x, y – x y 1 – y
Como estas medidas deben ser positivas
x > 0, y – x > 0 y 1 – y o, equivalentemente:
x > 0, y > x e y < 1
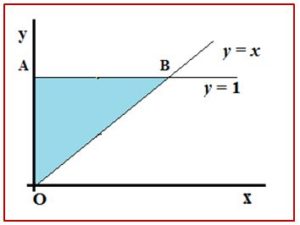
El problema está planteado en función de dos variables que representaremos en el plano. La región de los casos posibles está formada por los puntos (x, y), que cumplen las tres condiciones. Es el triángulo OAB en color azul
La región de los casos posibles es triangular y tiene 0,5 m2 de área.
Para que los tres trozos: x, y – x y 1 – y formen un triángulo deben cumplir la Desigualdad Triangular que impone que:

x < 0,5 y – x < 0,5 y 1 – y < 0,5 o, equivalentemente
x < 0,5 y < x + 0,5 e y > 0,5
Estas condiciones determinan la región de los casos favorables que a presentamos en amarillo sobre la de los casos posibles, es el triángulo A’B’C’ y tiene 0,125 m2 de área
Por lo tanto la probabilidad será:
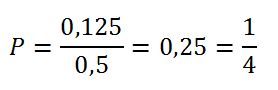
Que coincide con la Solución 1.




Gracias. Por cierto no está demás decir que esa es la solución dada por E. Lemoine publicada el año 1873 en Bulletin de la S.M.F.
Muchas gracias por su indicación, no conocía el dato, le diré que este problema, planteado como problema de probabilidades geométricas en tres dimensiones, lo descubri en el libro de E. Borel, R. Deltheil et Huron «Probalilités erreurs» (1923) de la Editorial Armand Colin y me pareció interesante resolverlo en geometria bidimensional y tridimensional.