La palabra fractal fue introducida en la literatura matemática en el año 1975 por B. Mandelbrot (1924-2010) para designar objetos de estructura irregular y fragmentada. Procede del término latino fractus (que significa quebrado). Se pueden considerar objetos fractales muchas formas que aparecen en la naturaleza, como las nubes, los árboles o las montañas, porque son tan irregulares que no existe en la geometría euclidiana una figura que los represente.
La estructura anómala y compleja de los objetos fractales se repite a diferentes escalas, Es decir, que, por mucho que nos aproximemos al objeto o ampliemos alguna de sus partes, observaremos siempre la misma estructura compleja. Además, los objetos fractales tienen una característica peculiar, que es la de poseer dimensión no entera, que analizaremos más adelante.
Por otra parte, la Matemática Pura ha proporcionado muchos ejemplos de figuras fractales de gran complejidad que repiten su estructura por autosemejanza, como la curva de Koch, la de Peano o de la Hilbert. Con el Sistema de Funciones Iteradas (SFI), que se basa en el principio de autosemejanza se pueden obtener figuras geométricas tales que cada una de sus partes es semejante a la figura completa, como en el caso del helecho M. Barnsley obtenido mediante cuatro transformaciones lineales en el cual, cualquiera de sus hojas, es una réplica exacta del helecho completo.
El pistoletazo de salida del estudio de los conjuntos fractales lo dio Mandelbrot en su artículo de 1967 titulado ¿Cuánto mide la costa de Gran Bretaña? Auto-Semejanza estadística y dimensión fractal. La pregunta parece inocente, pero dejó perplejos a sus colegas asistentes a un congreso.
El antecedente de estas ideas está en el matemático y pacifista F. Richardson (1881-1953) que, desde 1940 recopiló datos sobre la economía, la política, el crecimiento, etc de diferentes las naciones con el fin de encontrar estadísticamente las causas de las guerras y cómo prevenirlas.

En una parte secundaria de sus estudios observó que los datos sobre las longitudes de las fronteras eran muy diferentes y que, dependiendo de los datos de un país u otro, aparecían diferencias de hasta un 20 %. Por ejemplo, la frontera entre España y Portugal era 987 o de 1214 kilómetros según los datos procedieran de un país o de otro.
Observó que la razón de estas diferencias se debía al hecho de que, a medida que se reducía la unidad con la que se realizaba la medición de la frontera, iban apareciendo elementos, accidentes y detalles, que incrementaban la longitud de la frontera. Primero el contorno de un monte que no se tuvo en cuenta, luego el perímetro del saliente del monte y que con una unidad de medida aún más pequeña había que tener en cuenta el contorno de la piedra del saliente del monte; con unidades menores se podía apreciar el perímetro del grano de arena en la piedra del saliente del monte y así hasta el diámetro de las moléculas de sílice del grano de arena de la piedra del saliente del monte, etc, etc.
La geometría clásica no podía describir objetos naturales tan rugosos y quebrados como las fronteras de Richardson o como el contorno accidentado del litoral de Mandelbrot. Una cosa era parecía segura: Todo dependía de la unidad de medida y que, cuanto menor fuera la unidad (u), mayor sería la longitud medida (L(u)).
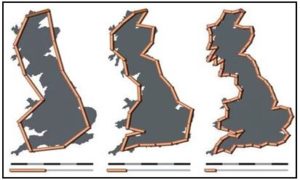
Los resultados que se obtuvieron de la longitud de la costa de Gran Bretaña con diferentes unidades de medida como se muestra en la figura son, de izquierda a derecha: 2350 km, 2775 km y 3425 km. Se aprecia aquí una sustancial diferencia de longitud de esta costa a medida que se reducen sucesivamente a la mitad las unidades de medida.
Richardson observó en su estudio sobre las medidad de las fronteras que su longitud aumentaba en función del grado de precisión con el que se realizaba la medida. Es decir, la longitud de la fronteras era mayor cuanto menor era la abertura del compás (unidad de medida) con que se medían las fronteras.
Midió las longitudes para diversas aberturas y para cada abertura, u , obtenía una longitud diferente, L(u), y observó que la longitud parecía crecer indefinidamente cuando u → 0. Tratando de encontrar una ley que relacionara la lunidad de medida con la longitud obtenida, representó gráficamente los puntos (log (u), log L(u)) y observó que se ajustaban a una recta de pendiente negativa:
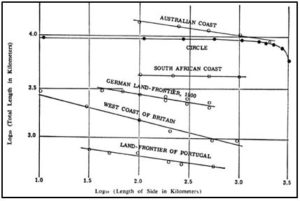
a) Que la longitud, L(u), aumentaba indefinidamente cuando la unidad de medida, u, tendía a cero
b) Que tomando logaritmos y representando gráficamente en el eje OX log (u) en el eje OY log L(u), los puntos (log (u), log L(u)) se ajustaban a una recta de pendiente negativa de ecuación:
log L(u) = – a·log (u) + b, (1)
con a y b positivos y 0 ≤ a < 1. Tal y como se observa en la figura con las costas de diferentes países.
La expresión (1) es equivalentemente [haciendo b = 10c] a:
L(u) = c·u-a (2)
Lo que significaba que la longitud de una costa, medida con una unidad u, era proporcional a u-a y que el coeficiente a era in coeficiente característico de cada costa.
Según declara Mandelbrot, su primera contribución a los fractales la realizó cuando en su obra relacionó el coeficiente a con la dimensión fractal de Hausdorff-Besicovitch, que denotamos con D y definió el concepto sencillo e intuitivo de dimensión de homotecia, que no había sido descrito con anterioridad, transformando la expresón (2) en la siguiente:
L(u) = c·u1-D donde 1 < D = 1 + a < 2
La dimensión de homotecia introducida por Mandelbrot se puede justificar intuitivamente de la siguiente forma:
- Si un segmento rectilíneo lo dividimos en n partes iguales que no se solapen, cada una de las partes puede deducirse del segmento total mediante una semejanza de razón r(N) =1/N (u =1/N)
La razón de semejanza, 1/N, es la unidad de medida, u, para que el segmento mida N unidades de longitud.
- Si un cuadrado lo dividimos en N cuadrados iguales que no se solapen, cada uno puede deducirse del cuadrado total mediante una semejanza de razón r(N) =1/N 1/2 .
La razón de semejanza, 1/N 1/2, es la unidad de medida, u, para que el cuadrado mida N unidades de superficie.
- Igualmente si un cubo lo dividimos en N cubos iguales que no se solapen, cada uno puede deducirse del cubo total mediante una semejanza de razón r(N) =1/N 1/3
Y también la razón de semejanza, 1/N 1/3, es la unidad de medida, u, para que el cubo mida N unidades de volumen.
En un espacio D-dimensional se cumplirá también que la razón de semejanza, 1/N 1/D, es la unidad de medida, u, para que el cubo D-dimensional mida N unidades D-dimensionales.
Todos cumplen que r(N) = 1/N 1/D ⇒ N = r -D
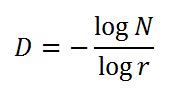
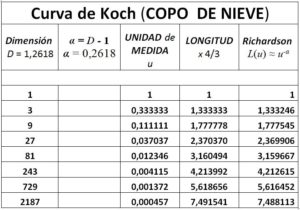
La complejidad geométrica que hemos descrito en la medida de una costa puede simplificarse y modelizarse mediante curva de Koch. Cuya construcción es la siguiente:
Partamos de un segmento rectilíneo de lado unidad P0. Dividimos el segmento en tres partes iguales de longitud 1/3 cada una y sustituyamos el segmento central por dos segmentos de igual longitud y obtenemos curva poligonal P1 de longitud 4·(1/3)= 4/3. Repetimos la operación con cada uno de los cuatro nuevos segmentos, es decir, con cada uno de los lados y obtenemos así la curva P2 de longitud (4/3)·(4/3)=16/9.
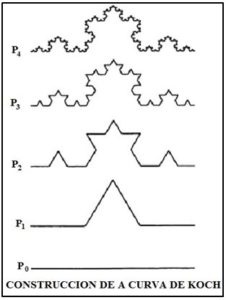
Repitiendo indefinidamente el proceso obtenemos una curva de longitud infinita, ya que en cada etapa su longitud se multiplica por 4/3. La iteración indefinida nos proporciona la isla de Koch o Copo de Nieve
Hay quien dice que si la curva de Koch estuviera viva sería imposible aniquilarla, puesto que sus trozos serían iguales a la curva original y renacería de cualquiera de sus más pequeños fragmentos como surge la vida en el universo.
La curva de Koch fue clasificada en la matemática como curva patológica por ser continua y, a pesar de ello, no era derivable en ninguno de sus puntos y se mantenía que no tenía ningún interés concreto y así lo podría suscribir un físico. Era una curva demasiado irregular para la geometría y la física clásicas.
Sin embargo, la geometría fractal proporciona una nueva visión. La curva Copo de Nieve puede ser un modelo simplificado de la geometría de una costa. Si la curva no es aceptable plenamente para representar una costa, no es porque sea demasiado irregular, sino porque, en comparación con una costa real, su irregularidad es demasiado sistemática, es decir, que su desorden no es excesivo, sino insuficiente.
La dimensión de la curva Copo de nieve es un valor entre 1 y 2.
Como cada parte se deduce del todo como una homotecia de razón 1/3, si a la unidad le aplicamos una homotecia de razón 1/3 y salen cuatro partes iguales, luego:
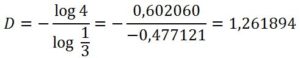
La curva Copo de Nieve tiene ese nombre porque si la iteración se hace partiendo de los lados de un triángulo equilátero produce la siguiente figura:
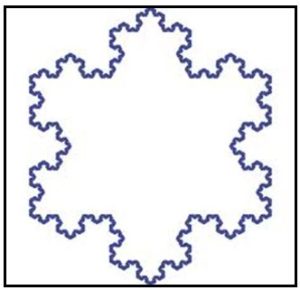
A continuación se da la siguiente tabla dónde se relaciona a la longitud de la curva de Koch calculada a partir de la a de Richardson ( Tomando como a, D–1) y la longitud de cada iteración.