Las iteraciones se han utilizado en matemáticas desde la antigüedad. Procesos iterativos clásicos son el algoritmo de Euclides para calcular el máximo común divisor, los métodos del punto fijo para resolver ecuaciones de forma aproximada, el cálculo de la raíz cuadrada o el cálculo del factorial de un número por multiplicaciones sucesivas.
En un método iterativo para resolver ecuaciones se repite el mismo procedimiento de mejora sobre una solución aproximada inicial, x0 , que se suele elegir arbitrariamente y llama de semilla. Con ésta se realizan una serie de cálculos para obtener una aproximación mejor. La fórmula que permite construir la aproximación se conoce como ecuación de recurrencia y el nombre de iteración procede de que la repetición sucesiva del proceso, pero utilizando como semilla la aproximación obtenida en cada paso.
Ejemplo: Resolver, aplicando el método de iteración de punto fijo, la siguiente ecuación 2x -5x + 2 =0.
Sin entrar en problemas de convergencia, tenemos que 5x = 2x +2, por tanto,

Partiendo del valor inicial o semilla x0 = 0, obtenemos:
x0 = 0, x1 = f (x0) = f(0) = 0,6, x2 =f (x1) = f(0,6) = 0,703, x3 = f (x2) = f(0,703) = 0,726
x4 = f (x3) = f (0,726) = 0,731, x5 = f (x4) = f(0,731) = 0,732, x6 = f (x5) = f(0,732) = 0,732
La solución de la ecuación pedida es x ≈ 0,732
Precisamente en el método iterativo del punto fijo, que se ha utilizado para resolver esta ecuación, está el origen histórico de los fractales de B. Mandelbrot (1924-2010) y, más precisamente, en el método de Newton-Raphson. Si la ecuación es f(x) = 0, el método de Newton-Raphson consiste en partir de un valor inicial x0 que se introduce en la ecuación de recurrencia:
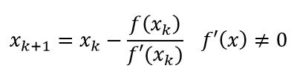
obteniendo así un resultado x1. Ese nuevo valor se vuelve a introducir en la misma expresión, obteniendo un nuevo resultado x2, y así, sucesivamente, calculamos x0, x1, x2, …, xn, … . Sin detenernos en cuestiones de convergencia, cada vez que introducimos uno de los resultados intermedios en esa expresión obtenemos una aproximación mejor de la solución de la ecuación f(x) = 0.
En 1879 el matemático inglés A. Cayley (1821-1895) estudió ecuaciones de variable compleja y, en particular, la ecuación polinómica en el plano complejo z3 – 1 = 0 y propuso determinar las cuencas de atracción de las raíces de la misma (es decir, el conjunto de puntos, z0 que convergen asintóticamente a cada una raíz de sus tres raíces) utilizando el método de Newton. Cada raíz de z3 – 1 = 0 actuaría como atractor para todos los puntos de su cuenca.

Para acercarnos a estos conceptos nos serviremos del siguiente ejemplo, más, sencillo con la ecuación z = z2. Nos aproximaremos al estudio de las raíces de la ecuación y estudiamos la iteración, comenzando con la semilla z0, La iteración zn+1= zn2 nos permite clasificar todos los puntos del plano complejo C,
Si z0 es un número genérico del cuerpo de los números complejos C y lo expresamos en forma polar: z0 = r·eiq
z0 = r·eiq , z1 = r2·[eiq]2 , z2 = r3·[eiq]3, z3 = r4·[eiq]4,…, zn = rn+1·[eiq]n+1,…
- Si el módulo de la semilla r < 1, el módulo irá disminuyendo en cada iteración hasta tomar valor r = 0 para n infinito, es decir hasta el (0,0i).
- si r >1 el módulo aumentará exponencialmente, hasta infinito.
- Si r = 1, los valores de la iteración estarán en una circunferencia de radio unidad sobre el plano complejo.
Por lo tanto, todos los números del plano complejo que están en el interior del círculo unidad, (r < 1) forman el conjunto prisionero P que sería la cuenca atracción de (0,0i); las iteraciones sucesivas de los números que verifican (r >1) tienden al infinito y forman el conjunto de escape E. Finalmente, los números complejos de módulo unidad, r =1, que forman la circunferencia unidad son la frontera de ambos conjuntos.
En casos más complicados se han obtenido objetos geométricos fractales que se conocen como conjuntos de Julia. En honor a uno de los pioneros, P. Fatou (1878-1929) y G. Julia (1893-1978) que, a finales del siglo XIX, estudiaron los métodos iterativos y obtuvieron profundos resultados matemáticos y no llegaron más lejos, seguramente, por carecer de ordenadores (el sino de los tiempos).
Fatou y G. Julia abordaron el problema propuesto por el Cayley para ecuaciones de variable compleja y estudiaron las cuencas de atracción de las raíces del polinomio z3-1 = 0 en el plano complejo por el método de Newton-Raphson. Las soluciones de la ecuación z3-1 = 0 , son: {1, e2p/3, e4p/3}. Cayley pretendía saber dónde terminaría la iteración infinita (la órbita) de un punto zo arbitrario. P. Fatou y G. Julia demostraron que las fronteras de las cuencas de atracción estaban enormemente enredadas y su distribución sobre el plano complejo era extraordinariamente compleja.
Fatou (1878-1929) trabajó en la dinámica de análisis complejos. Se graduó en 1901, y entró a trabajar en el Observatorio de París. Fatou continuó sus investigaciones matemáticas y estudió los procesos iterativos y, de forma particular funciones de variable compleja del tipo fc(z) = z2 + c. dónde c era un número complejo cualquiera y en el caso de que z0 = 0, es decir la ecuación de recurrencia:
zn = (zn-1)2 + c con la semilla z0 = 0
Este problema sería, medio siglo más tarde, retomado por B. Mandelbrot utilizando ordenadores y mostrando su genial visión geométrica de los proceso numéricos para generar representaciones gráficas del comportamiento en el plano complejo de esta sucesión para cada punto c. Creando una nueva rama de las matemática, la Geometría Fractal y mostrando un conjunto de belleza singular conocido como conjunto de Mandelbrot.
Debido a las limitaciones impuestas por la extensión de los trabajos expuestos en este blog no entraremos en detalles sobre prioridades en la consecución de resultados entre estos dos grandes matemáticos franceses, ya que lo que tratamos es destacar son sus logros en el terreno de la iteración sin disponer de computadoras.
Julia, en su articulo Mémoire sur l’itération des fonctions rationnelles, al estudiar las funciones fc(z) = z2 + c, explicó cómo se podía construir un conjunto cuya frontera era imposible de dibujar por tener, entre otras propiedades, longitud infinita. Precisamente se llama conjunto de Julia, J(fc), para cada valor de c, a la frontera infinita, delgada e irregular entre el conjunto de puntos que tienden a infinito tras una serie de iteraciones (conjunto Exterior de Julia) y los que se estabilizan en un punto o en una órbita (conjunto Interior de Julia).
Entre otros resultados obtuvieron los siguientes teoremas:
Teorema: Si z0 es la semilla de zn = (zn-1)2 + c y, además se verifica que |z0 | > max {2, |c|} la órbita de z0 por J(fC ) es infinita.
Lo que significa que si |z0 | > max {2, |c|}, entonces z0 escapa a infinito por la iteración zn = (zn-1)2 + c y que la frontera del conjunto de todos los puntos del plano que tienen esa propiedad el conjunto de Julia asociado a c
También demostraron, en cierta medida, que los conjuntos de Julia eran autosemejantes, es decir, tenían la propiedad de que cada parte era una imagen reducida del conjunto entero, como una coliflor, y que había unos conjuntos de Julia conexos (intuitivamente, formados por una sola pieza) y otros que no los eran y probaron el siguiente teorema:
Teorema: Si la órbita del origen, z0 = (0,0) es acotada el conjunto de Julia, J(fC ) es conexo
Este teorema fundamental le permitió a B. Mandelbrot (1924 -2010) representar en el ordenador todos los valores de c que hacían que el conjunto de Julia J (fC ), fuera conexo y descubrir un conjunto de gran complejidad y belleza, llamado Conjunto de Mandelbrot.
Se llama Conjunto de Mandelbrot al conjunto de los c tales que la órbita:
z0 = 0, zn = (zn-1)2 + c está acotada
Por ejemplo, si c = 1 la sucesión 0, 1, 2, 5, 26… diverge, luego c = 1 no pertenece al conjunto de Mandelbrot. En cambio, si c = -1 la sucesión 0, -1, 0, -1, … es acotada y, por tanto, c = -1 pertenece al conjunto de Mandelbrot.

Mandelbrot fue el creador de la Geometría Fractal, que surgió en la década de 1970 con ayuda de los ordenadores. Mandelbrot conocía los trabajos de Julia y Fatou y utilizó los medios informáticos para realizar iteraciones y analizarlas, pero su gran visión e intuición geométrica, también contribuyeron a la creación de esta nueva materia. En 1982 publicó su libro: La Geometría Fractal de la Naturaleza, en el que explicaba la génesis y el progreso de sus investigaciones en este campo.
La Geometría Fractal presenta un modo nuevo de acercarse al estudio de las irregularidades de la naturaleza En lugar de buscar patrones para representar los objetos naturales entre formas geométricas platónicas, abstractas, ideales y externas a la propia naturaleza de los objetos que observamos , la Geometría Fractal busca relaciones armónicas internas entre las partes que lo forman cuando se examina el objeto a diferentes escalas. De esta forma, con la Geometría Fractal, se estudia el aspecto del objeto en cada escala. Y, siguiendo la clasificación de las geometrías de F. Klein (1849-1925), la Geometría Fractal es la geometría que estudia los aspectos geométricos que permanecen invariantes con el cambio de escala. Es decir, estudia la autosemejanza de los objetos. Esta propiedad es importante, ya que nos permite predecir el comportamiento futuro de un objeto fractal, puesto que, por el principio matemático de autosemejanza, crecerá y se replicará de forma idéntica infinitas veces a distintas escalas.
Víctor Arenzana Hernández




