Los Juegos de Corro son diversiones inocentes en las que los niños, cogidos de la mano, giran y bailan en círculos al compás de canciones que ellos mismos cantan. En los juegos se suele seguir una coreografía marcada por las instrucciones de la canción. En España hay una enorme cantidad de estos Juegos, como, por ejemplo el corro de la patata, la gallinita ciega, o el patio de mi casa. Un Juego de Corro no lúdico y bastante más siniestro es el conocido como Juego de Josefo.
Flavio Josefo (37-101) en su libro La guerra de los judíos, nos dejó un interesante problema de matemáticas que ha tenido muchas variantes en los juegos de niños y al que han dedicado su atención grandes matemáticos. G. Cardano (1501-1576) en Practica Arithmeticae Generalis (1539) recogió una versión del juego llamándola ludus Josephi, y este nombre se ha conservado hasta nuestros días. L. Euler (1707-1783) fue el primero en encontrar, en 1775, leyes de recurrencia para resolver el problema en diferentes casos.
Josefo pertenecía a la aristocracia sacerdotal de Jerusalén y en el año 63 fue enviado a Roma para conseguir la liberación de varios sacerdotes que habían sido hechos prisioneros y enviados a Roma por el Gobernador de Judea Félix y cumplió su objetivo gracias al apoyo de Popea, la esposa de Emperador Nerón. A su vuelta a Jerusalén, en el año 65, la relación de los judíos con Roma se había hecho más tensa y la guerra parecía inevitable. El Sanedrín, para prepararse para la guerra contra Roma, dividió Judea en siete demarcaciones militares y Josefo fue nombrado gobernador de Galilea.
La guerra se desató al año siguiente y duró hasta el año 73. Es este contexto de guerra fue en el que cuenta Josefo que, después de que los romanos hubieran tomado Jotapata, ciudad de la Baja Galilea, él y cuarenta galileos más se refugiaron en una cueva y fueron cercados por los romanos. Para evitar ser capturados y vendidos como esclavos, los galileos prefirieron morir y, para cumplir esta macabra decisión, decidieron que se colocarían en círculo con los lugares numerados y se matarían entre ellos con una espada siguiendo el siguiente procedimiento: el primero mataría al segundo y pasaría la espada al tercero, el cual acabaría con al cuarto, pasaría la espada al quinto y así se seguía el ciclo sucesivamente, hasta que quedara uno solo, el cual se quitaría la vida él mismo.
Josefo, que tenía una buena formación matemática, calculó el lugar que debía ocupar el último superviviente, se colocó en esa posición y logró convencer al penúltimo superviviente para que se entregaran juntos a los romanos y así evitar los dos la muerte.
Cuando Josefo se entregó a Tito Flavio Vespasiano, justificó su actuación diciéndole que tenía que comunicarle un mensaje de los cielos, que era que pronto sería Emperador y así sucedió tras la muerte de Nerón en el año 68. El vaticinio se cumplió, Vespasiano fue Emperador y Josefo fue liberado y llevado a Roma a ocupar un cargo del Imperio hasta su muerte en el año 101.
La historia tiene claroscuros sobre la veracidad de la historia de Josefo y de su buena elección de su posición ante la muerte en círculo de sus compañeros, también hay dudas sobre las razones por las que Josefo, que tenía excelentes relaciones con Roma, fue nombrado por el Sanedrín gobernador militar de Galilea en tiempos de guerra, pero lo cierto es que dejó planteado un bonito problema matemático.
Antes de tratar calcular cómo supo Josefo la posición que debía ocupar entre los cuarenta y un judíos para librarse de la muerte, nos acercaremos al problema analizando casos más sencillos, con un número menor de individuos.

Si n = 4 : En la primera vuelta comienza el 1, morirían el 2 y el 4 y la espada volvería al 1, que en la segunda vuelta acabaría con el 3 y se salvaría. De forma esquemática (señalo en negrita el lugar del individuo que en cada vuelta se queda con la espada para matar al siguiente):
1 2 3 4 → 1 3 → 1
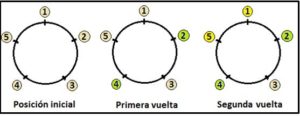
Si n = 5: En la primera vuelta morirían el 2 y el 4 y la espada quedaría en el 5, que en la segunda vuelta acabaría con el 1 y luego pasaría la espada al 3 que acabaría con el 5 y se salvaría el 3. De forma esquemática:
1 2 3 4 5 → 1 3 5 → 3 5 → 3
Analizaremos el problema de forma más general dividiéndolo en dos casos:
CASO 1.- El número de individuos es potencia de dos, esto es, n = 2m. Empezaremos con casos sencillos siguiendo las reglas del juego de Josefo:
- Si n = 23 = 8: 1, 2, 3, 4, 5, 6, 7, 8 → 1, 3, 5, 7 → 1, 5 → 1
- Si n = 24 = 16: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ,11, 12, 13, 14, 15, 16 → 1, 3, 5, 7, 9, 11, 13, 15 → 1, 5, 9, 13 → 1, 9 → 1
- Si n = 25 = 32: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 → 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31 → 1, 5, 9, 13, 17, 21, 25, 29 → 1, 9, 17, 25 → 1, 17 , → 1
Observamos que, cuando damos la primera vuelta y se eliminan los números pares, el 1 se queda con la espada. Como quedan un número par de individuos (quedaran 2m-1) en la segunda vuelta, se eliminan los números que ocupan lugar par contando desde el 1, que vuelve a quedarse con la espada. Damos la tercera vuelta al círculo (quedaran 2m-2), y nuevamente la número 1 se libra de la eliminación. Y finalmente, cuando quedan sólo dos, el 1 y otro, el 1 se salvará.
CASO 2.- Si n no es potencia de dos. Necesariamente n = 2m + k con m > 0 y 0 < k < 2m. (Si k = 0, entonces n = 2m y si k = 2m, n = 2m + 2m = 2·2m = 2m+1 ).
Como en el caso primero empezaremos con casos sencillos:
- Si n = 22+ 1 = 5: 1, 2, 3, 4, 5 → 1, 3, 5 → 3, 5 → 3
- Si n = 22+ 2 = 6: 1, 2, 3, 4, 5, 6 → 1, 3, 5 → 1,5 → 5
- Si n = 22+ 3 = 7: 1, 2, 3, 4, 5, 6, 7 → 1, 3, 5, 7 → 3, 7 → 7
- Si n = 23+ 1 = 9: 1, 2, 3, 4, 5, 6, 7, 8, 9 → 1, 3, 5, 7, 9 → 3, 7 → 3
- Si n = 23+ 2 = 10: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 → 1, 3, 5, 7, 9 → 1, 5, 9 → 5,9 → 5
- Si n = 23+ 3 = 11: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 → 1, 3, 5, 7, 9, 11 → 3, 7, 11 → 7, 11 → 7
- Si n = 23+ 4 = 12: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12 → 1, 3, 5, 7, 9, 11 → 5, 9, 1 → 9, 1 → 9
- Si n = 23+ 5 = 13: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13 → 1, 3, 5, 7, 9, 11, 13 → 3, 7, 11 → 3, 11 → 11
- Si n = 23+ 6 = 14: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 11, 12, 13, 14 → 1, 3, 5, 7, 9, 11, 13 → 1, 5, 9, 13 → 5, 13 → 13
- Si n = 23+ 7 = 15: o1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 → 1, 3, 5, 7, 9, 11, 13, 15 → 3 , 7, 11, 15 → 7, 15 → 15
El procedimiento para resolver el problema cuando n = 2m + k consiste en tratar de reducirlo al caso anterior para ello se han de eliminar siguiendo las reglas del juego de Josefo. Para ello eliminaremos los elementos k elementos que ocupan los lugares pares: 2, 4,…, 2k y nos quedarán 2m elementos. Es decir, cuando hayamos eliminado k elementos estaremos ante el primer individuo de un nuevo círculo de 2m elementos. Ese individuo ocuparía la posición 2k +1 en el círculo inicial. Y ese será el puesto que debe ocupar un individuo para salvarse
En el caso de Josefo los individuos los 41 individuos 41 = 25 + 9, por tanto k = 9, eliminamos individuos hasta que queden 32. En este caso habrá que eliminar los elementos que ocupen los lugares pares: 2, 4, 6, 8, 10, 12, 14, 16, 18, entonces quedan 32 = 25 individuos y el primero de este nuevo círculo ocupa el lugar 19 (19 = 2·9 +1) y esa será la posición que eligió Josefo para librarse de la muerte.