
Problema 1.- Probar que el cuadrado de cualquier entero impar da resto uno al dividirlo por 8
Solución: Cualquier número entero a es de la forma 4k, 4k+1, 4k+2, 4k +3, siendo k entero, por consiguiente, cualquier entero impar, a, se puede expresar en la forma 4k+1 o 4k+3, elevando al cuadrado:
a2 = (4k+1)2 = 16k2 + 8k +1 = 8(2k2 + k) +1 es múltiplo de 8 más uno, que da resto 1 al dividirlos por 8
a2 = (4k+3) = 16k2 + 24k + 9 = 8(2k2 + 3k) +1, igual que el anterior ,es múltiplo de 8 más uno, que da resto 1 al dividirlos por 8.
Problema 2.- Probar que n2+1 nunca puede ser múltiplo de tres
Solución: Cualquier número entero n es de la forma 3k, 3k+1, 3k+2
1.- Si n = 3k, entonces n2 = 9k2 por lo que n2 +1 = 9k2+1, que es múltiplo de 3 más uno
2.- Si n = 3k+1, entonces n2 = 9k2+6k +1 = 3(3k2+2k)+1, n2 +1 = 3(3k2+2k) +2 que es un múltiplo de 3 más dos.
3.- Si n = 3k+2, entonces n2 = 9k2+12k + 4 = 3(3k2+4k +1) +1, por lo que
n2 +1 = 3(3k2+ 4k +1) + 2 que es un múltiplo de 3 más dos.
Problema 3: Demostrar que no existe ningún valor entero n para el que 15 divida a (3n+77)
Solución: Para que 15 divida a m = 3n + 77, tiene que se múltiplo de tres
Evidentemente, m = 3n + 77 = 3 (n+25) + 2, que es un múltiplo de tres más dos para cualquier valor de entero de n y darían resto 2 al dividir m entre tres
Problema 4.- Probar que el producto de 3 números consecutivos es siempre un múltiplo de 6?
Solución: Se propone como ejercicio
Problema 5.- El producto de cuatro enteros consecutivos es múltiplo de 24
Solución: Veremos que el producto de cuatro enteros consecutivos es divisible por 8 y por 3 a la vez.
- En el producto de cuatro números consecutivos:
P = n (n+1) (n+2) (n+3)
Es siempre múltiplo de 8, ya que en P hay siempre dos factores pares (y, además, uno o dos factores que son múltiplos de tres)
Como hay dos factores pares y son consecutivos uno será de la forma 2p y otro de la forma 2p +2, con p entero, y el producto:
2p (2p +2) = 4 p (p+1) = Múltiplo de ocho,
ya que p o (p+1) es par y, por tanto, p (p+1) es múltiplo de dos.
- Veremos que P = n (n+1)(n+2) (n+3) es múltiplo de 3.
El resto de la división de un número entero cualquiera entre tres puede dar 0, 1, o 2. Como en el producto P = n (n+1)(n+2) (n+3). En los cuatro factores consecutivos al dividir entre 3 se darán los tres restos (y alguno se repetirá), por lo tanto, uno de los factores (o dos) será múltiplo de tres, por tanto:
P = n (n+1)(n+2) (n+3) es múltiplo de tres,
por lo tanto, P = n (n+1)(n+2) (n+3), que es múltiplo de tres y de ocho, es múltiplo de 24.
Problema 6.- El producto de cinco enteros consecutivos: n (n+1)(n+2) (n+3)(n+4)
es múltiplo de 120.
Observación: El número de combinaciones de n elementos elementos tomadas de 5 en cinco son:
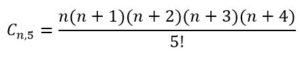
Es decir: n (n+1) (n+2) (n+3) (n+4) = 120 Cn,5
Como el número de combinaciones es un número entero y 5! =120:
n (n+1) (n+2) (n+3) (n+4) es un múltiplo de 120
Problema 7: Probar que N = n5 – 5n3 + 4n es divisible por 120, para n >2
Solución: Basta con observar la factorización de N en cinco enteros consecutivos:
N = n5 – 5n3 + 4n = n (n4 – 5n2 + 4) = n (n2-1) (n2– 4) = (n-2)(n-1)n(n+1)(n+2)
Y aplicar el resultado del ejercicio anterior




