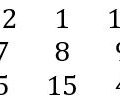PROBLEMAS ARITMÉTICOS CON EL 2020

PROBLEMA 1.- Los enteros positivos se escriben en orden sucesivo en líneas horizontales según la siguiente regla. En el primero colocamos el 1, después, en cada fila escribimos doble cantidad de números que en la línea anterior (como se muestra a continuación) ¿En qué línea queda hemos escrito el  número 2020? ¿Cuál es su posición dentro de ella?

Solución: Los números se escriben en la siguiente disposición:

1

2   3

4   5   6   7

8   9  10 11 12  13 14  15

16 ….      

Observemos que la primera fila empieza en 2⁰, la segunda en 2¹, la tercera en 2², la enésima empieza en 2^n-1, por lo tanto. como

2¹⁰ < 2020 < 2¹¹      ya que    1024 < 2020 < 2048

Por lo tanto 2020 está en el renglón 11.

En fila 11 el número 2020 ocupa el lugar 2020 – 1023 = 997

PROBLEMA 2.– ¿Cuál es la cifra decimal que ocupa el lugar 2020 en el desarrollo decimal de a) 4/101?     b) ¿En 1/13?  y       c) En 1/43?

Solución:

a) El número 4 /101 = 0,0396 0396 0396 0396 0396 0396…, tiene un periodo de cuatro cifras: 0396. En 2020 hay 2020:4 = 505 periodos exactamente, luego la cifra que ocupa el lugar 2020 es seis.

b) El número 1/13 = 0,076923 076923 076923 076923 076923 … el periodo es de seis cifras: 076923, como 2020 : 6 = 336 + 4   en 2020 hay 336 periodos y cuatro cifras más, por lo tanto la cifra que ocupa el lugar 2020 será  9.

c) El número 1/43 = 0, 023255813953488372093 023255813953488372093… el periodo es de veintiuna cifras  023255813953488372093, como 2020 : 21 = 96 + 4   en 2020 hay 96 periodos y cuatro cifras más, por lo tanto la cifra que ocupa el lugar 2020 será  2

PROBLEMA 3.- Se escriben en sucesión todos los números del 1 al 2020, en orden, uno a continuación del otro, para formar un número N, es decir,

N = 1234567891011121314…20012002…2020.

1. ¿Cuántas cifras tiene N?
2. ¿Qué posición ocupa la cifra central dentro del número N ?
3. ¿Cuál es la cifra central de N?

Solución:

1. ¿Cuántas cifras tiene N? Hay nueve números de una cifra, noventa de dos, novecientos de tres… y de 2000 a 2020 hay  1021 números de cuatro cifras. Luego el número N tiene:  1·9 + 2·90 + 3·900 + 4·1021 = 9 + 180 + 2700 + 4084 = 6973 cifras
2. ¿Qué lugar ocupa la cifra central? 6973:2 = 3486,5    ⇒ la cifra central  ocupa el lugar
3. Para de terminar la cifra central razonaremos así: Con números menores de 4 cifras tenemos  1·9 + 2·90 + 3·900 = 2889 cifras de N y necesitaremos x los números de cuatro cifras que nos den hasta las 3487 cifras que necesitamos:

2889 + 4 x = 3487    ⇒    4x = 598    ⇒    x = 149,5

(teniendo en cuenta que los números de cuatro cifras comienzan en 2000), la cifra central será la segunda cifra de 2149, es decir, 1.

PROBLEMA 4.- Calcular la suma:

1·2⁰ + 2·2¹ + 3·2² + 4·2³ + … + 2020·2²⁰¹⁹

Solución: Expresaremos la suma de forma recurrente:

a_n = n 2^n-1    y     a_n+1 = (n+1) 2ⁿ =  n 2ⁿ +  2ⁿ    ⇒ 

⇒      a_n+1 = 2 a_n + 2ⁿ

Se pueden escribir los 2020 términos de la suma,  partir de a_n+1 = 2 a_n + 2ⁿ, dando a n los valores 1, 2, 3, …, 2019,  de este modo:

a₁  =          1

a₂  = 2 a₁ + 2

a₃  = 2 a₂ + 2²

. . . . . . . . . . . .

a₂₀₂₀ =   2 a₂₀₁₉ + 2²⁰¹⁹

Sumando miembro a miembro:

S =a₁ + a₂ + a₃ + …+ a₂₀₂₀ =  2(a₁ + a₂ + a₃ + …+ a₂₀₁₉) + (1 + 2 + 2² +… +2²⁰¹⁹).

El primer paréntesis es S – a₂₀₂₀ , el segundo es una suma de términos en progresión geométrica de razón 2, de donde:

S = 2(S – a₂₀₂₀) + (2²⁰²⁰ – 1) =  [ ya que a_n = n 2^n-1]=

2(S – 2020·2²⁰¹⁹) + (2²⁰²⁰ – 1) =

= 2S – 2020·2²⁰²⁰+ 2²⁰²⁰ – 1=

Despejando S

S = 2019·2²⁰²⁰+1