Los problemas de edades han sido, junto con los problemas de móviles, de relojes, de repartos y de mezclas, los tópicos que han llenado los libros de Aritmética. Los problemas de edades son útiles para ejercitarse y profundizar en el manejo del sistema de numeración posicional, porque, en algunos de ellos, se necesita manejar el valor de las cifras según la posición que ocupan o la descomposición de un número en factores y siempre son un estimulante ejercicio para la mente porque los problemas de edades nos hacen analizar el lenguaje oral y examinar evolución de de las variables en el tiempo.
A continuación se exponen cuatro problamas
Problema 1.– Calcula la edad que tenía Juan el año 2000 si la edad que tenía entonces era igual a la suma de las cifras de su año de nacimiento.
SOLUCIÓN: Juan nació el año 19ab en el año 2000 tendría la edad:
2000 – 19ab = 2000 -1900 – ab = 100 – 10a – b,
Que, como debe ser igual a la suma de las cifras del año de nacimiento, se tiene que:
100 – 10a – b = 1 + 9 + a + b ⇒ 90 = 11a + 2b
Como a y b son cifras tienen que ser números enteros positivos tales que
0 ≤ a ≤ 9 y 0 ≤ b ≤ 9
Por tanteo:
a no puede ser 1 ⇒ 79 = 2b ⇒ b tendría dos cifras
a no puede ser 2 ⇒ 68 = 2b ⇒ b tendría dos cifras
a no puede ser 3 ⇒ 57 = 2b ⇒ b no sería entero
a no puede ser 4 ⇒ 46 = 2b ⇒ b tendría dos cifras
a no puede ser 5 ⇒ 35 = 2b ⇒ b no sería entero
a no puede ser 6 ⇒ 24 = 2b ⇒ b tendría dos cifras
a no puede ser 7 ⇒ 13 = 2b ⇒ b no sería entero
Si a = 8 ⇒ 2 = 2b ⇒ b = 1 (solución válida)
a no puede ser 9 ⇒ -9 = 2b ⇒ b no sería entero ni positivo
Luego la solución es a = 8 y b = 1 el año de nacimiento será 1981 y en el año 2000 tenía 19 años [ 1 + 9 + 8 +1 = 19]
Un problema análogo
Problema 2.- Calcula la edad que tiene una persona de más de 20 años si la edad que tiene en 2019 es igual a la suma de las cifras del año de su nacimiento.
SOLUCIÓN: Nació el año 19ab en el año 2019 tendrá la edad:
2019 – 19ab = 2000 – 1900 + 19 – 10a – b, que,
como debe ser igual a la suma de las cifras del año de nacimiento, se tiene que:
100 + 19 – 10a – b = 1 + 9 + a + b ⇒ 109 = 11a + 2b
![]()
Ahora, por tanteo, buscaremos un a entero, talque 0 ≤ a ≤ 9 y 109 – 11a sea par y b cumpla que 0 ≤ b ≤ 9. La solución será a = 9 ⇒ b = 5. Luego nació en 1995 y en 2019 tendrá 24 años
Problema 3.- Las edades de los cinco miembros de una familia (padre madre y tres hijos) son números primos menores de 45 y el producto de las cinco edades es un número de seis cifras formado por las cifras que forman la edad del padre repetidas tres veces ¿Cuál será la edad de la madre? ¿Cuál será la edad padre si es mayor que la madre?
SOLUCIÓN: La edad del padre será ab .
El producto de las cinco edades será:
ababab = ab·10000 + ab·100 + ab = ab (10000 + 100 + 1) = ab 10101
Como la edad del padre es ab, el producto de las edades de los tres hijos y la madre será 10101, que descomponiéndolo en factores primos queda:
10101 = 3·7·13·37
La edad de la madre será 37 y la de los hijos: 3, 7 y 13 respectivamente:
Si la edad del padre será un primo p tal que 37 < p < 45 ⇒ p = 41, 43, luego el padre tendrá 41 o 43 años.
Problema 4.- Luis le dice a Juan:” Yo tengo el doble de la edad que tú tenías cuando yo tenía la edad que tú tienes y cuando tú tengas la edad que yo tengo, la suma de nuestras edades será 63 años”. Hallar la edad de Luis.
SOLUCIÓN: Resumimos los datos en la tabla:
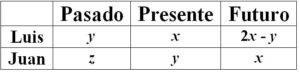
En el presente: Luis tiene una x años de edad y Juan y años
En el pasado: Cuando Luis tenía y años Juan tenía z años.
El enunciado nos dice que x = 2z (1), pero, además, nos dice que x – y = y – z y, además que ese valor coincide con la diferencia de edades entre Juan y Luis. Esa relación la podemos expresar en la forma: x – 2 y + z = 0 (2)
En el futuro; Juan tendrá la edad x años y Luis x + (x – y) = 2x – y años. Y el enunciado nos dice que La suma de las edades será 63, es decir: 3x– y = 63 (3)
Las ecuaciones (1), (2) y (3) nos resuelven el problema:
Eliminando la z entre (1) y (2) queda: 3x – 4y = 0
Resolviendo el sistema formado por esta ecuación y la ecuación (3)
![]()
y = 21, x = 28, son, respectivamente, las edades de Juan y Luis.