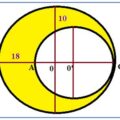
PROBLEMA 1. Dado un cuadrado ABCD de lado 8 cm, se construye un círculo que pasa por los vértices consecutivos A y D y es tangente al lado BC en su punto medio. Calcular el radio, R, del círculo.
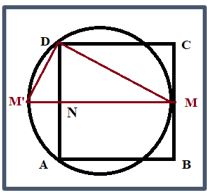
Respuesta:
El triángulo M’DM es rectángulo en D por ser ángulo inscrito en la circunferencia y abarcar un ángulo de 180º. Por el teorema de la altura, la altura DN relativa a la hipotenusa. verifica la proporción (observemos que el segmento NM es igual al lado del cuadrado, por lo tanto, mide 8 cm y la altura relativa la mitad del mismo y medirá 4 cm), llamando a M’N = x:
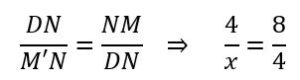
x =2 ⇒ MM’ = 10 ⇒ R = 5 cm
x =2 ⇒ MM’ = 10 ⇒ R =5
PROBLEMA 2.- ¿Cuál es la mayor área posible para un triángulo, conociendo que dos de sus lados miden, respectivamente, a = 5 cm y b = 12 cm?
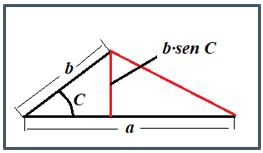Respuesta: El área será cuando los lados a y b sean perpendiculares. En cualquier caso, si tomamos el lado a como base, la altura nunca superior a b = 12.
Por otra parte, si recordamos la fórmula en la que interviene la trigonometría; El área de un triángulo es igual a la mitad del producto de dos de sus lados por el seno del ángulo que determinan
Área = (a·b·sen C)/2
Dados los lados a y b el área será máxima cuando sen C = 1, ⇒ C = 90º
Área = (5·12)/2 = 30 cm2
Este triángulo rectángulo es pitagórico, porque su hipotenusa mide 13 cm, que es un número entero.
PROBLEMA 3.- Dado un cuadrado de lado 8 cm, dos semicircunferencias con centro en la mitad del lado y radio 4 cm y una circunferencia inscrita en el cuadrado. Calcula el área de la superficie sombreada
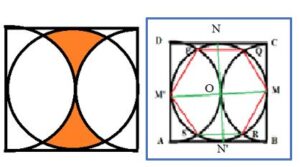
Respuesta:
Área del sector OPQ = (Base x altura)/2 = (2π4/6)4/2 = 16π/6 = 8π /3 cm2
Área de segmento circular de base PQ = Área del sector OPQ – Área del triángulo equilátero OPQ =
= 8π/3 – 4√3 = (8π – 12Ö3)/3 cm2
Área del triángulo curvilíneo OPNQ = Área del sector OPQ – 2 (Área de segmento circular de base PQ) = 8π/3 – 2(8π – 12√3)/3 = (24√3 – 8π)/3 cm2
El área de la figura sombreada será: 2(24√3 – 8π)/3 cm2
PROBLEMA 4.- Demostrar que cinco puntos cualesquiera en el interior de un triángulo equilátero de lado 2 cm, siempre habrá dos de ellos que están a una distancia menor o igual que 1 cm.
Respuesta: Utilizaremos el Principio del Palomar. Sabemos que la distancia máxima entre dos puntos en el interior de un triángulo equilátero es menor que o igual que el lado.
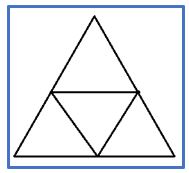
El triángulo equilátero de lado 2 cm se puede dividir en cuatro triángulos equiláteros de lado 1cm como se indica en la figura.
Por lo tanto, si tenemos cinco puntos en el interior de un triángulo equilátero de lado 2 cm, dos de ellos deben estar dentro de un triángulo de lado uno y, por tanto, la distancia entre ellos debe ser menor o igual que 1 cm
