PROBLEMAS ELEMENTALES DE TEORÍA DE NÚMEROS

La Teoría de Números es una disciplina fundamental dentro de las Matemáticas. Desde Pitágoras el número ha sido el concepto fundamental alrededor del cual han pivotado las Matemáticas. La Teoría de Números es considerada como  una  disciplina fundamental que ocupa dentro de las matemáticas una posición tan prominente como la que  disfrutan las propias Matemáticas entre las demás ciencias. La Teoría de Números estudia los números (fundamentalmente enteros)  y sus propiedades, en particular se ocupa de los  número primos, de la divisibilidad, de los sistemas de numeración, de la combinatoria, de las fracciones continuas , de las congruencias,  de las ecuaciones diofánticas,  de la criptografía  y de otros muchos temas que son fundamentales para el estudio de las Matemáticas.

Hoy presento cuatro problemas de divisibilidad

PROBLEMA 1.- Demuestra que  el producto de 4n enteros consecutivos es divisible por 2³ⁿ.

Solución: Entre 4n enteros consecutivos hay 2n números pares. Sacando factor común en cada uno queda un factor 2²ⁿ, pero en  2n números pares hay n múltiplos de 4, lo que supone  2ⁿ número de doses más N = 2²ⁿ·2ⁿ·N’  = N = 2³ⁿ·N’

PROBLEMA 2.-  Demuestra que  N = 14n³  + 9n² + n es múltiplo de seis si  n ≥ 1.

Solución:   N = 14·n³  + 9·n²  + n = n (14n² + 9n + 1) =

(Factorizando el trinomio de segundo grado)

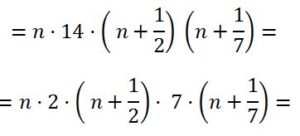
= n·(2n + 1) (7n + 1).

Para que N sea múltiplo de seis debe ser múltiplo de dos y de tres

1. Veamos que N es múltiplo de dos:

Si n es par, n = 2t (t entero)   ⇒ N = 2t·(4t· + 1)·(14t + 1) ⇒  N es múltiplo de 2 (ya que el factor  2t es par)

Si n es impar, n = 2t+1   ⇒  N = (2t·+1)(4t· + 3)·(14t + 8) ⇒ N es múltiplo de 2 (ya que el factor (14t + 8) es par)

1. Veamos que N es múltiplo de tres

Si n es múltiplo de tres, n = 3t    ⇒   N= 3t·(6t + 1) (21nt+ 1)  ⇒  N es múltiplo de tres

Si  n = 3t +1   ⇒   N = (3t·+1)(6t + 3)·(21t + 8)   ⇒   N es múltiplo de 3 (ya que el factor  (6t + 3) es múltiplo de tres)

Si  n = 3t – 1   ⇒   N = (3t – 1)(6t -1)·(21t – 6)   ⇒   N es múltiplo de 3 (ya que el factor  (21t – 6)   es múltiplo de tres)

PROBLEMA 3.- Demuestra que N = a ⁿ⁺⁴ – aⁿ  es múltiplo de 10

Solución: Consideremos las siguientes factorizaciones de N:

N = a ⁿ⁺⁴ – aⁿ  =  aⁿ (a ⁴ – 1) = aⁿ (a ² + 1)(a ² – 1) =

= aⁿ (a ² + 1)(a +1)(a  – 1)

Para que N sea múltiplo de diez debe ser múltiplo de dos y de cinco.

1. Primero veamos que N es par: (a puede ser par o impar)

Si a es par   ⇒    aⁿ es par   ⇒   N  es múltiplo de dos

Si a es impar   ⇒    a ² es impar   ⇒    (a ² + 1) es par ⇒   N  es múltiplo de dos.

1. Veamos que N es múltiplo de cinco: (a puede dar cinco restos diferentes al dividirlo entre 5), por lo tanto se pueden producir los siguientes casos:

Si a = 5 t    ⇒  ((5t)ⁿ es múltiplo de cinco)   ⇒  N es múltiplo de cinco

Si a = 5 t + 1    ⇒   N = (5 t + 1)ⁿ [(5 t + 1) ²+ 1] (5 t + 2)·5t    ⇒  N es múltiplo de cinco, ya que el factor  5t es múltiplo de cinco).

Si a = 5 t + 2   ⇒  N = (5 t + 2)ⁿ ((5 t + 2) ²+ 1) (5 t + 3)· (5 t + 1) =

(5 t + 2)ⁿ (25 t² + 20t + 5)(5 t + 3)· (5 t + 1)  ⇒ N es múltiplo de cinco, puesto que el factor  25 t² + 20t + 5 = 5(5 t² + 4t + 1) es múltiplo de cinco.

Si a = 5 t + 3  ⇒(5 t + 3)ⁿ ((5 t + 3) ²+ 1) (5 t + 4)· (5 t + 2) =

(5 t + 3)ⁿ (25 t² + 30t + 10) (5 t + 4)· (5 t + 2)  N es múltiplo de cinco, ya que el factor  25 t² + 30t + 10 = 5 t² + 6t + 2) es múltiplo de cinco)

Si a = 5 t – 1  ⇒ (5 t – 1)ⁿ ((5 t – 1) ²+ 1) (5 t – 2)·5t, ya que el factor  5t es múltiplo de cinco

PROBLEMA 4.- Demuestra que si n es impar y N = n (n + 2)(25n² – 1)², entonces N es múltiplo de 24.

Solución: Para que N = n(n + 2)(5n + 1)(5n – 1) sea múltiplo de veinticuatro debe ser múltiplo de tres y múltiplo de ocho.

N es múltiplo de tres y analizaremos los siguientes casos:

• Si n es múltiplo de tres, n = 3t ⇒ N = 3t(3t + 2)(15t + 1) (15t – 1) es múltiplo de tres
• Si n = 3t +1 ⇒   N = (3t +1)(3t +3)(15t + 6)·(15t + 4)   ⇒   N es múltiplo de 3 (ya que el factor  (3t+3) es múltiplo de tres)
• Si n = 3t – 1 ⇒   N = (3t -1)(3t + 1)(15t -4)·(15t – 6)   ⇒   N es múltiplo de 3 (ya que el factor  (15t – 6)   es múltiplo de tres)

N es múltiplo de ocho y analizaremos los siguientes casos:

• Si n es par, n = 2t ⇒ N = 2t(2t + 2)(10t + 1) (10t – 1) es múltiplo de ocho, porque  2t y (2t + 2) son pares consecutivos y uno de ellos será múltiplo de cuatro.
• Si n es impar, n = 2t +1 ⇒ N = (2t +1)(2t + 3)(10t + 6) (10t +4)  ⇒   N  es múltiplo de ocho, ya que (10t + 6) y (10t +4) son pares consecutivos