En este artículo esbozaremos algunas de las propiedades el número de recorridos diferentes que se pueden hacer para ir de un punto a otro en una red cuadrangular formada por líneas horizontales y verticales. Si partimos de un punto O (0,0) hasta un punto A (a,b) el avance se realizará de forma que el desplazamiento en ningún tramo suponga retroceso, es decir, en sentido horizontal el desplazamiento será hacia a la derecha y en vertical hacia a arriba. Esto se puede expresar diciendo que del punto (x, y) se pasa a (x+1,y) o a (x,y+1) hasta alcanzar el punto A (a,b). Los desplazamientos que cumplen esta condición se llaman desplazamientos reticulares. A a + b se le llama longitud del desplazamiento
Cada camino para ir de O a A, ha de tener a + b tramos de los cuales a deben ser horizontales (que representaremos con h) y b verticales (que representaremos con v), cada camino se puede representar por una reordenación de a tramos horizontales y b verticales:
hhhh.. (a veces) … hh, vvvv.. (b veces) … vv
El número de trayectos es fácilmente calculable y se puede expresar en términos de números combinatorios como el número de permutaciones que pueden hacerse con a + b elementos de los cuales hay a iguales a h y b igual a v:
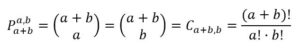
EJERCICIO 1: Cuántos desplazamientos reticulares diferentes habrá para ir del vértice O (0,0) de un cuadrado al vértice opuesto (a, a).
Respuesta:

Habrá (observando la figura)
En un cuadrado 1×1… C2,1 = 2
En un cuadrado 2×2 … C4,2 = 6
En un cuadrado 3×3 … C6,3 = 20
En un cuadrado 4×4 … C8,4 = 70
En un cuadrado 5×5 … C10,5 = 252
En un cuadrado axa … C2a, a
EJERCICIO 2: ¿Cuántos desplazamientos reticulares de longitud igual a n parten de (0,0)?
Respuesta: Como son desplazamientos reticulares y no hay retrocesos ni descensos en la trayectoria, un desplazamiento de longitud n partirá de (0,0) y llegará a un punto (a,b) de la retícula tal que a+b = n. Como a y b son enteros positivos esos puntos serán los de la diagonal:
A0(0, n), A1(1, n-1), A2(2, n-2), …, An-1 (n-1, 1), An(n, 0)
- Desplazamientos reticulares de O a A0: Cn ,0 = 1
- Desplazamientos reticulares de O a A1: Cn ,1 = n
- Desplazamientos reticulares de O a A2: Cn ,2 = n(n-1)/2
….
- Desplazamientos reticulares de O a An-1: Cn ,n-1= n
- Desplazamientos reticulares de O a An: Cn ,n= 1
El número total de desplazamientos reticulares de longitud n será la suma de los desplazamientos a todos los puntos:
Cn ,0 + Cn ,1 + Cn ,2 + ···· + Cn ,n-1 +Cn ,n-1
que la suma de los coeficientes del desarrollo del binomio de Newton (1+1)n = 2n, por lo tanto:
Cn ,0 + Cn ,1 + Cn ,2 + ···· + Cn ,n-1 +Cn ,n-1 = 2n
OBSERVACIÓN
a) El Desplazamientos reticulares para llegar a los puntos de la diagonal (0,1), (1,0) son respectivamente: C1,0 = 1, C1,1 = 1,
b) El número de caminos para llegar a los puntos de la diagonal (0,2), (1,1) (2,0) son respectivamente: C2,0 = 1, C2,1 = 2, C2,0 = 1
c) El número de caminos para llegar a los puntos de la diagonal (0,3), (1,2), (2,1) y (0,3) son respectivamente: C3,0 = 1, C3,1 = 3, C3,2 = 3, C3,3 = 1
d) El número de caminos para llegar a los puntos de la diagonal (0,4), (1,3), (2,2), (3,1), (4,0) son: C4,0 = 1, C4,1 = 4, C4,2 = 6, C4,3 = 4, C4,4 = 1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
…….
Que es el triángulo de Pascal
EJERCICIO 3

¿Cuántos desplazamientos reticulares puede hacer Rogelio, que vive en A, para ir a casa de su amigo Abelardo, que vive en B?
¿Cuántos si tiene que pasar por D?
¿Cuántos si Luis no quiere pasar por D porque está Luisito el Pelma y perdería demasiado tiempo?
Solución:
Recorridos diferentes para ir de A a B: Tendrá que hacer seis recorridos horizontales y cuatro verticales: h h h h h h v v v v. Las reordenaciones serán:
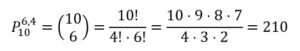
Recorridos diferentes para ir de A a B pasando por D: Para llegar de A a D: hhhhvv y para ir de D a B: hhvv.las reordenaciones serán:
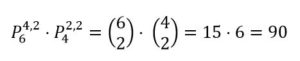
Recorridos diferentes para ir de A a B pasando por C: Para llegar de A a C: hhvvv y y para ir de C a B: aaaab
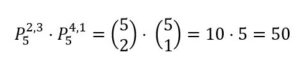
Recorridos para n pasar por quiere pasar por D porque está Luisito el Pelma 210 – 90 = 120 recorridos
EJERCICIO 4
¿Cuántos recorridos distintos puede hacer ratón R, Para comerse el queso que está en Q?
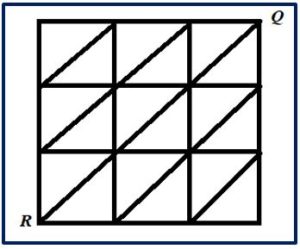
Solución:
Caso 1: Tres horizontales tres verticales: hhhvvv
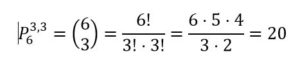
Cada vez que recorre un diagonal se evita una horizontal y otra vertical
Caso2: Una diagonal de las: dhhvv
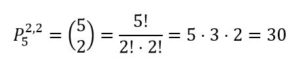
Caso 3: Dos diagonales de las ddab
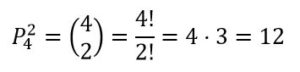
Caso 4: Tres diagonales: ddd: 1
Total = 20 + 30 + 12 + 1 = 63