Isaac Newton (1643-1727) pensaba que el espacio y el tiempo eran absolutos, lo que suponía admitir que el espacio existía con independencia de los objetos materiales que estaban en él. En la concepción newtoniana los cuerpos deambulaban en un espacio y en un tiempo absolutos y ambos escapaban a la observación.
Para G. Leibniz (1646-1717) el espacio no era que escapara a la observación simplemente era inobservable y, por tanto, afirmaba Leibniz, hablar de la existencia del espacio absoluto carecía de toda justificación y concebía un espacio (y un tiempo) relacional, que dependía de la materia, es decir, de los cuerpos contenidos en él y que sin materia no existían ni espacio ni tiempo.
Leibniz también ponía en tela de juicio la noción de atracción gravitatoria newtoniana que consideraba como una invención ficticia para explicar un hecho. La atracción gravitatoria era una ficción porque actuaba en un espacio inmaterial, el cual carecía de materia que permitiera transmitir su acción. Es decir, el espacio absoluto y vacío no podía ser medio de ninguna acción, y, por tanto, argumentaba Leibniz, que la física newtoniana se apoyaba en hipótesis inventadas. Newton tuvo en cuenta, de alguna forma, las críticas de Leibniz y, en el Escolio General de la segunda edición de los Principia (1687), afirmaba que él describía hechos y que no formulaba hipótesis (hypotesis non fingo).
A continuación, trataremos de destacar la importancia que tuvo la reformulación de la ley de gravitación universal de S. D. Poisson (1781-1840) a partir de la que enunció Newton, En la formulación de Poisson se dejaron de lado algunas consideraciones filosóficas sobre la naturaleza del espacio y el tiempo.
La ley de gravitación de Newton se transformó en la expresión ∇2g (x1,y1,z1) = 4πGρ, donde en el primer miembro se recogía la información sobre el espacio y las fuerzas observables a través de la geometría del mismo y en el segundo miembro de la ecuación aparecían unas constantes (4πG) multiplicadas por la densidad de masa ρ. Relacionando el espacio, expresado en forma geométrica, con los cuerpos masivos que en él se movían (la densidad de masa (ρ)).
A continuación realizamos un esquema del proceso de Poisson:
Para Newton transformación que tuvo la presentación de la gravitación según la formuló Newton al campo gravitatorio propuesto obtenido por Poisson Newton Fuerza de Gravitatoria entre dos masas M y m
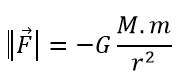G = 6, 6738480·10-11 m3/kg s2
Intensidad de campo creado por la masa M:
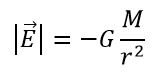Función potencial del campo es la función escalar f (x, y, z) = k/r, siendo k = G·M y
La intensidad de campo gravitatorio será:
La medida de la variación de la intensidad campo gravitatorio en un volumen determinado se calcula mediante la divergencia, la cual mide la diferencia entre el flujo saliente y el flujo entrante de un campo vectorial a través de la superficie que rodea a un volumen si el campo tiene fuentes la divergencia será positiva, y si tiene sumideros, la divergencia será negativa. La divergencia mide la variación neta con la que se dirige la materia al exterior de cada punto, y en el caso de ser la divergencia idénticamente igual a cero, describe al flujo incompresible del fluido
Teorema: Si el campo de fuerzas producido por una distribución de masas, viene por una función vectorial que es gradiente de una función escalar f(x,y,z), cumple ∇2 f= 0.
Ya que si la función vectorial es gradiente, el campo se llama conservativo
Sea R una región del espacio y S su frontera. Supongamos R que es esférica
Igualando (1) y (2) se obtiene
Primer miembro se recoge información sobre el espacio, las fuerzas observables y, en suma, sobre la geometría del mismo; en el segundo miembro constante y la densidad de masa, esto es la masa por unidad de volumen.
La ley de gravitación en la teoría de relatividad general tiene la misma estructura que la de Poisson. El primer miembro de la ecuación, Rab, que representa la curvatura geométrica del espacio-tiempo modificado por Einstein con el tensor métrico se obtiene el tensor, Rab, de Einstein y representa la geometría el espacio de tetradimensional. En el segundo miembro Tab es el tensor energía-impulso que representa la cantidad de energía y de movimiento que posee una distribución de materia o un campo. en una cierta región del espacio.
El primer miembro de la ecuación, Rab, que representa la curvatura geométrica del espacio-tiempo modificado por Einstein con el tensor métrico se obtiene el tensor, Rab, de Einstein y representa la geometría el espacio de tetradimensional. En el segundo miembro Tab es el tensor energía-impulso que representa la cantidad de energía y de movimiento que posee una distribución de materia o un campo. en una cierta región del espacio.
