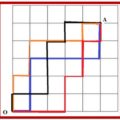
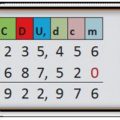
El Juego del Quince o Taken es un antiguo juego del tipo solitario que consiste en una cuadrícula de dieciséis casillas, 4×4, en la que se colocan los números del 1 al 15, dejando, por tanto, una casilla vacía.
Los números se pueden mover en la cuadrícula por deslizamiento. Un movimiento válido en el juego consiste en deslizar a la casilla vacía uno de los números adyacentes a la misma horizontal o verticalmente y ocuparla, dejando vacía la casilla que estaba ocupada originalmente por el número movido.
El problema que planteamos es decidir si, con las reglas del juego, a partir de cualquier disposición posible de los números, se puede obtener la cuadrícula básica, que es la que tiene los quince primeros números naturales ordenados de menor a mayor y la casilla en blanco en decimosexto lugar.
Samuel Loyd (1841-1911), que fue el mayor creador de acertijos, rompecabezas y problemas deingenio y ajedrez de los Estados Unidos.
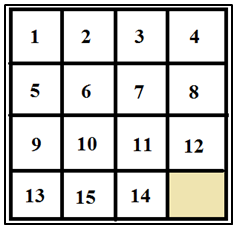
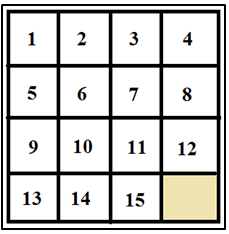
En 1878 planteó el problema de obtener, a partir de una permutación que se diferenciaba de la disposición básica primera solamente en la inversión de los números 14 y 15 (Figura 1), mediante movimientos admitidos en el juego, la permutación básica formada por los quince primeros números naturales ordenados de menor a mayor (Figura 2). (Pasar de la disposición de la figura 1 a la de la figura 2).
El ingenio y el prestigio de Sam Loyd como creador de rompecabezas y creador de problemas de ingenio era reconocido universalmente. Había publicado varios rompecabezas tales como el de piezas de cartón llamado los asnos engañosos o el parchesi (parchís) adaptación que hizo Loyd del juego tradicional hindú del mismo nombre. También Loyd se atribuyó el invento del rompecabezas conocido como Juego del Quince del que estamos hablando. El ingenio de Loyd no tenía límites, como lo prueba la patente que hizo en 1896 de su invención mecánica, Borrado de la faz de la Tierra.
Planteado en forma matemática, Sam Loyd proponía la cuestión siguiente: Si a partir de de cualquiera de las
16!= 20.922.789.888.000
permutaciones posibles del juego era posible pasar a permutación básica realizando los movimientos válidos que permitía el juego.
Para contestar a la cuestión analizaremos lo que sucede cuando hacemos un movimiento válido, pero antes afinaremos un poco el vocabulario estableciendo los siguientes conceptos:
- Se llama permutación de un conjunto de n elementos a cada una de las diferentes ordenaciones que se pueden hacer con esos elementos.
- Dada una permutación, diremos que dos elementos están en inversión cuando su orden difiere del de la permutación principal (o permutación de referencia).
- Una permutación es de orden par cuando tiene un número par de inversiones y será de orden impar cuando tiene un número impar de inversiones.
- Para calcular la paridad de una permutación se procede de la forma siguiente: Comenzando por la izquierda se compara cada elemento con los que tiene a su derecha, contando cada vez que nos encontramos con una inversión.
Ejemplo de cálculo de la paridad de una permutación: Partiendo de la permutación principal (1,2,3,4,5,6), entonces las inversiones de la permutación (3,6,1,2,5,4) se calculan así:
El 3 está invertido con el 1 y con el 2 (dos inversiones). El 6 está invertido con 1, 2, 4 y 5 (cuatro inversiones). El 1 no está invertido con ninguno de los que le siguen. El 2 tampoco está invertido con ninguno de los números que le siguen. El 5 está invertido con el 4 (una inversión). En total (3,6,1,2,5,4) tiene siete inversiones respecto a (1,2,3,4,5,6), luego es permutación impar.
Cuando hacemos un movimiento válido sucede: lo siguiente:
- Los movimientos horizontales no modifican en nada la permutación numérica ya que sólo desplazan la casilla vacía dentro de la misma fila.
- Si desplazamos un número hacia abajo para ocupar la casilla vacía, el número adelanta a los tres que le siguen (luego la nueva permutación difiere de la primera en tres inversiones) y la permutación resultante tendrá paridad diferente a la de partida, además, la casilla vacía pasará de ocupar una fila impar a una fila par o
- De modo análogo, si desplazamos un número hacia abajo éste retroceda tres puestos y la permutación resultante tendrá paridad diferente a la de partida, la casilla vacía pasará de una fila impar a una fila par o viceversa.
Por lo tanto, aplicando estas consideraciones al problema propuesto vemos que Sam Loyd, se propone pasar con los movimientos válidos de una permutación impar como
(1,2,3,4,5,6,7,8,9,10,11,12,13,15,14) a otra par (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15).
Este juego se publicó en los periódicos entre 1880 y 1882 y su resolución despertó el entusiasmo de muchas personas en Estados Unidos, ya que se ofreció un premio a quien resolviera, pero pronto se vio que era un problema no resoluble. Afirmación que se puede demostrar atendiendo a la paridad de las permutaciones de la siguiente forma:
La primera permutación tiene una inversión (14,15), luego será impar, y la segunda ninguna, por tanto será par. Además, las dos permutaciones tienen la casilla vacía en la misma posición (casilla 16), por lo tanto, el número de movimientos verticales realizados tiene que haber sido par, ya que la casilla vacía debe haber subido y bajado las mismas veces.
Por lo tanto, la paridad de la permutación ha cambiado un número par de veces (y cada vez tres inversiones), lo cual equivale a decir que quedó con la misma paridad que al principio (o sea impar). Por lo tanto no era posible llegar a la cuadrícula a principal que es par.