Un punto fijo de una transformación es un punto que permanece invariable (se transforma en sí mismo) bajo la transformación. Las translaciones en el plano son movimientos que no tienen puntos fijos; un giro de centro O y ángulo α tiene un único punto fijo, el centro O; en una simetría axial de eje e el eje e es una recta de puntos fijos.
Un punto c se dice que es fijo para la función f de un conjunto en sí mismo si cumple la propiedad f (c) = c, es decir, si c permanece invariable o, en otras palabras, si c se transforma en sí mismo o bien la imagen de c coincide con c.
Así, la función f : R → R , f(x) = x2– x tiene dos puntos fijos: x = 0 y x = 2 puesto que f(0) = 0 y f(2) = 2
Gráficamente, los puntos fijos de la función y = f(x), f: R → R, están determinados por los puntos de corte de la gráfica de la función y = f(x) con la recta y = x.
En la gráfica se puede observar que la función y = f(x) que transforma la recta real unidimensional en ella misma tiene tres puntos fijos c, c’ y c’’.

Los teoremas de punto fijo tienen mucha importancia en matemáticas. Un teorema de punto fijo es un enunciado que garantiza la existencia (y unicidad) de un punto fijo de una función dada que aplica un conjunto M sobre mismo [f: M → M].
Deseamos saber si existe algún punto en c ϵ M tal que f (c) = c
Habitualmente se habla del Teorema del Punto Fijo de Brouwer, en honor al matemático holandés L.E. Brouwer (1881-1966), aunque no fue el primero en demostrar un teorema de punto fijo. Para dimensión n = 1, en 1817, B. Bolzano (1781-1848) demostró un teorema de punto fijo; en 1909 Brouwer enunció un teorema para n = 2 y n = 3; en 1910 el matemático francés J. Hadamard (1865 – 1963) lo enunció para una dimensión n arbitraria; pero en 1912, Brouwer realizó diversas formulaciones y demostraciones del mismo por las que se le considera uno de los creadores de la topología moderna.
La forma más simple del teorema de punto fijo supone la hipótesis, que la función f es continua y definida de un intervalo cerrado y acotado, [a, b], en sí mismo.
Teorema de punto fijo (n=1): Si f es una función continua en [a, b] y f (x) ϵ[a, b] para todo x ϵ[a, b], entonces f tiene por lo menos un punto fijo en [a, b].
Si exigimos, además, la existencia de derivada, f ’(x), para todo x ϵ (a, b), y |f ’(x)| ≤ K < 1 , siendo K constante, entonces f tiene un único punto fijo x ϵ [a, b].
Además, se cumple la propiedad de que, dado un x0 ϵ (a,b) cualquiera, la sucesión x0 , x1 , x2 , … definida por la iteración: x1= f(x0), x2 = f(x1), x3 = f(x2), …, xn = f(xn-1), … converge al punto fijo c con independencia del punto x0ϵ(a,b) por el que se comience la iteración. Esta iteración se llama Iteración del Punto Fijo.
Conocer si una función tiene un punto fijo tiene una serle de aplicaciones importantes.
- Se utiliza para resolver ecuaciones del tipo f (x ) = 0, transformándolas en otras ecuaciones equivalentes del tipo, x = g(x), mediante la iteración xk+1 = g(xk), cumpliendo que | f ’(x)| <1, a partir de un cierto valor inicial x0 hasta que se cumpla el criterio de parada elegido o se haya realizado el número de iteraciones máximo admitido.
Por ejemplo: Para resolver la ecuación f(x) = x – cos x = 0 en el intervalo [0,π/2 ] por el método de Iteración del Punto Fijo expresamos la ecuación f (x ) = 0 en la forma x = g(x), es decir, ennuestro caso, x = cos x, como su derivada, -sen x, cumple |sen (x)| < 1 la iteración xk+1 = cos (xk), tiene un punro fijo partiendo del cualquier valor inicial, tomando x0= 0,5 radianes y haciendo cincuenta iteraciones se obtiene:
x0= 0,5, x1 = 0,8776, x2 = 0,6390, x3 = 0,8027, x4 = 0,6848, x5 = 0,7682, x6 = 0,7192,
x7 = 0,7524, x8 = 0,7301, x9 = 0,7451, x10= 0,7350, x11= 0,7418, x12 = 0,7372, x13 = 0,7403,
x14 = 0,7382, x15 = 0,7396, x16 = 0,7387, … …. x50= 0,73908513…
que se acerca cada vez más al punto fijo, solución de la ecuación f(x) = x – cos x = 0
- También se emplea para realizar demostraciones de existencia de soluciones en ecuaciones diferenciales. El Teorema de Picard transforma el problema de valor inicial:
x’(t) = f(t, x(t)) (t ∈ [a, b]),
x(t0) = x0.
En un problema equivalente
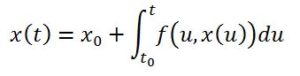
Donde da las condiciones para que se pueda encontrar por iteración la función x(t). La forma integral es útil para demostrar teoremas de existencia.
- Si consideramos que la función y = f(x) es una transformación que cambia de posición los elementos del eje OX y los coloca en la posición que ocupan en el eje OY, como si todos los puntos de OX se reubicaran, podemos interpretar en la figura que todos los puntos de OX han cambiado de posición salvo los puntos c, c’ y c’’.
Bajo ciertas condiciones las transformaciones continuas tienen puntos fijos. Lo que tiene consecuencias en la vida real para funciones en tres dimensiones. Por ejemplo: Si revolvemos un vaso de agua con una cucharilla tanto como queramos, por el Teorema del Punto Fijo, habrá al menos una molécula de agua que ocupe exactamente el mismo lugar en que se encontraba antes de que empezamos a revolver.
- A veces tiene consecuencias curiosas como el Teorema de la Bola Peluda que garantiza la existencia de un punto que no es como todos. Y que sólo su existencia tiene consecuencias de enorme repercusión. Para aproximarnos a al teorema
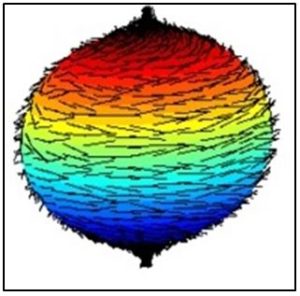
Supongamos una esfera cubierta de pelo, el Teorema nos dice que no se puede peinar la esfera de forma que los pelos estén orientados de forma continua y que siempre habrá, en alguna parte, un remolino, una raya, etc. y que, por lo tanto, tanto no se puede peinar de forma perfecta y siempre habrá algún remolino, raya o ruptura de peinado. Pensemos en un peinado en el cual todos los pelos que se encuentren sobre el ecuador de la bola se inclinan hacia el oeste.
A medida que avanzamos en latitud del Ecuador hacia los Polos, orientaremos, poco a poco, la alineación de los pelos hacia los polos, hasta que los pelos que se encuentran sobre cada polo queden en posición vertical (siguiendo el Eje de la Tierra). Todo esto parece muy poco útil y alejado del mundo real, pero no es cierto.
El Teorema de la Bola Peluda con una formulación tan impresionante como ésta:
«Un campo vectorial continuo definido sobre una esfera de dimensión par, al menos igual a 2, se anula en al menos un punto.»
O, equivalentemente, el Teorema en dimensión dos:
No existe un campo vectorial continuo sobre la esfera que sea no nulo en todos los puntos.
Lo que significa que si suponemos que la esfera es la Tierra, y que los vectores del campovectorial continuo representa la dirección del viento sobre la superficie terrestre en un momento dado, el Teorema nos dice que siempre, habrá algún remolino, tornado o ciclón en alguna parte.