TEORÍA DE NÚMEROS: A VUELTAS CON LOS DIVISORES DE UN NÚMERO ENTERO

En este trabajo haremos un recordatorio de algunas  cuestiones de Aritmética y Teoría de Números que se abordaban  que se abordaban  en los Planes de Estudios de Matemáticas de Bachillerato en España  hace ya cincuenta años. Cuando en la Enseñanza no había aparecido la informática y tampoco  las calculadoras

PROBLEMA 1.- Calcula los divisores de un número n cuya descomposición en factores primos es:  n = a^x·b^y·c^z,

Respuesta: Obsérvese que, como a, b y c son números primos, un divisor cualquiera estará formado por algunos factores a, b, c con exponentes respectivos menores o iguales que x, y, z . Para obtenerlos todos bastará escribir:

(1, a, a², a³ …. a^x)

(1, b, b², b³ …. b^y)

(1, c , c², c³ …. c^z)

Formando todos los productos que se puedan obtener tomando uno y un solo elemento de cada fila, se forman todos los divisores de n.  Como cada fila tiene 1+x, 1+ y 1+z elementos, el número total de divisores será:

Dn = (1+x)(1+y)(1+z)

PROBLEMA 2.- Calcula la suma de los divisores del número n = a^x·b^y·c^z,

Respuesta: Como los divisores de n son todos los productos posibles de las componentes de los vectores del ejercicio anterior, la suma de todos los divisores posibles vendrá dada por la expresión

SDn = (1+ a+ a² +···  +a^x)(1+ b+ b² +···+ b^y )(1+ c + c² +···+ c^z ) =

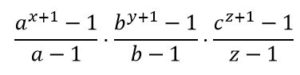
PROBLEMA 3.- Calcula la suma de los divisores del número 720

Respuesta: Como 720 = 2⁴·3²·5, aplicando la fórmula anterior:

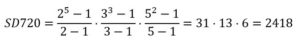
PROBLEMA 4.- Calcula la suma de los divisores de un número 150

Respuesta: Como 150 = 2·3·5², el número 150 tiene 12 divisores.

SD150 = (1+ 2)(1+3 )(1+5+5²) = 3·4·31= 372

PROBLEMA 5.- Calcula el producto de los divisores de 150

Respuesta: Como 150 = 2·3·5², el número 150 tiene 12 divisores Dn = 2·2·3 = 12 y los divisores son :  1, 2, 3, 5, 6, 10,15, 25, 30, 50, 75,150.  Puede observarse que las parejas (1·150), (2,·75), (3,50), (5,30), (6,26) y (10,15) tienen el mismo producto: 150, por tanto:

PD150 = 150⁶ = 11.390.625.000.000

PROBLEMA 6.- Calcula el producto de los divisores de 100

Respuesta: Como 100 = 2²·5², el número 100 tiene 9 divisores Dn = 3·3 =9 y los divisores son:  1, 2, 4, 5, 10 ,20, 25, 50, 100  (tiene un número impar de divisores). Puede observarse que las parejas (1, 100), (2, 50), (4, 25) y (5, 20), tienen el mismo producto: 100 y queda el término central 10 , por tanto:

Ejercicio: Demostrar que el producto de los divisores de un número n que tiene m divisores es:

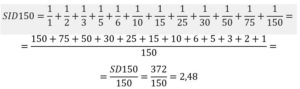
PROBLEMA 7.-Calcula la suma de los inversos de los divisores del número 150

Respuesta: 150 = 2·3·5². Número de divisores de 150 = 2·2·3 =12

Los divisores de 150 son: 1, 2, 3, 5, 6, 10,15, 25, 30,50, 75,150