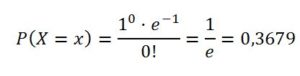En una ocasión el jugador de béisbol Bill Buckner dijo una frase que describe de forma clara el aspecto del cálculo de probabilidades que quiero destacar la frase es: el beisbol es un juego de los promedios, pero en un corto período de tiempo, tener un poco de suerte no es algo malo.
Lo que Buckner quería destacar es que cuando un fenómeno sucede por término medio, por ejemplo, una vez al año no significa que ocurra todos los años una vez. Puede haber unos años que no se produzca, mientras que otros años puede aparecer varias veces. Por esa razón podemos preguntarnos cuál es la probabilidad de que un año no se presente el fenómeno.
Problemas de este tipo fueron estudiados por S. D. Poisson (1781-1840), descubriendo la distribución de Poisson, que es una distribución de probabilidad discreta que permite calcular, a partir de la frecuencia media de que ocurra un suceso, la probabilidad que ese suceso aparezca un determinado número de veces en cierto periodo de tiempo. El resultado lo dio a conocer en 1838 en su obra Recherches sur la probabilité des jugements en matières criminelles et matière civile. (Investigación sobre la probabilidad de los juicios en materias criminales y civiles).
A continuación se exponen dos ejercicios el uno de simple aplicación y otro de resolución mediante procedimientos del cálculo de probabilidades
Ejercicio 1: Si un banco recibe en promedio 6 cheques sin fondo por día, ¿cuál es la probabilidad de que reciba, cuatro cheques sin fondo en un día dado determinado?
Solución: Podemos aplicar la fórmula de Poisson:
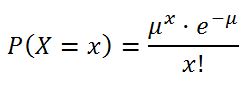
Donde X es la v.a. “número de cheques sin fondo que llegan al banco un día cualquiera {0, 1, 2, 3,…, n}”; x es “el número de cheques sin fondo que llegan al banco en un día cualquiera concreto, en nuestro caso x = 4, µ es la media de cheques sin fondo por día, en nuestro caso µ = 6 y e = 2.718…
Por tanto:
![]()
Ejercicio 2: En cierto cruce de una ciudad se produce un choque entre dos vehículos una vez al año como media, ¿Cuál será la probabilidad de que no se produzca un choque a lo largo de un año?
Solución: Como µ = 1, la probabilidad de que el choque se produzca un mes determinado del año será 1/12 y si dividimos el año en n partes iguales, la probabilidad de que se produzca en una de esas partes será 1/n, la probabilidad de que no se produzca en una de esas n partes será:
![]()
Y la probabilidad de que no se produzca en n partes de año será:

Si se divide el año en un número infinito de partes:
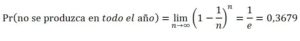
Aplicando la fórmula de la distribución de Poisson (µ= 1, x = 0) se obtiene el mismo resultado: