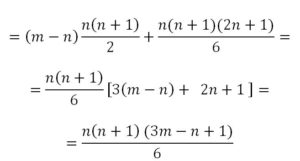
Nicómaco de Gerasa (60-120) fue el autor de la obra Isagoge Aritmética (Introducción a la Aritmética), que fue el primer tratado en el que la Aritmética apareció como disciplina autónoma e independiente de la Geometría. La obra de Nicómaco se mantuvo viva a través de a las traducciones latinas de Apuleyo de Madara (s. II) y del neoplatónico Boecio (480 – 524). En la Aritmética medieval el propósito de las obras Aritmética, como la de Boecio en De institutione musica y en De arithmetica, era el estudio teórico y práctico de la Aritmética, pero sus uso, en ocasiones, entraba en el campo de la numerología y superaba esa intención, ya que presentaba la visión platónica del orden y de la armonía matemática que regían el Universo.
Pero a través de la Aritmética también se transmitía en la Edad Media una afición por el juego intelectual que practicaban los monjes y la nobleza culta que buscaba ejercitar la inteligencia y apreciar la estética de la proporción en la música, en la arquitectura y en la pintura. De forma general, a través de la Aritmética se aportaban las teorías estéticas de belleza y placer visual, que influyeron notablemente sobre las ideas estéticas posteriores.
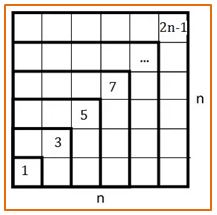
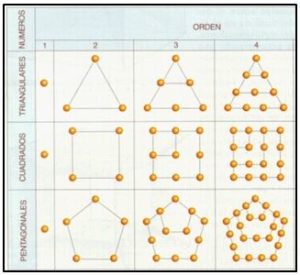
En el Capítulo 9 de De Aritmética, Nicómaco definió los números poligonales, en particular estudió las propiedades de los números cuadrados. Descubrió una relación fundamental que era que todo cuadrado era suma de números impares consecutivos
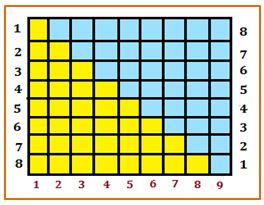
En segundo lugar, con una disposición similar de los números se podía calcular la suma de los n primeros números naturales. Un rectángulo de dimensiones (n+1)·n tiene un área igual al doble de la suma de los de los n primeros números impares como puede observarse en el caso del rectángulo de dimensiones 9×8. Por lo tanto, la suma de los n primeros números naturales será (n+1)·n/2.
La Aritmética también tenía otras representaciones geométricas para el cuadrado de una suma como, por ejemplo, para representar la identidad: (n+1)2= n2+2n +1
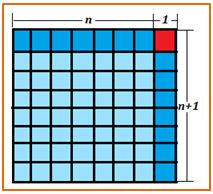
A partir de (n+1)2= n2 + 2n +1, dando valores sucesivos a n, se obtiene:
n = 0: 12= 02 + 2·0 +1
n = 1: 22= 12+ 2·1 +1
n = 2: 32= 22+ 2·2 +1
n = 3: 42= 32+ 2·3 +1
···
n = n: (n + 1)2 = n2+2·n +1
Sumando y simplificándolos cuadrados:
(n + 1)2 = 2·(1 + 2 + 3+ ··· + n)+ n +1
De dónde (n + 1)2 = 2·Sn + n + 1 ⇒ 2·Sn = (n + 1)2 – n – 1 ⇒
![]()
También por este procedimiento, a partir del desarrollo de (n+1)3= n3 + 3n2 + 3n + 1 podríamos calcular la suma de los cuadrados de los n primeros números, dando valores sucesivos a n, se obtiene
n = 0: 12= 03 + 3·02 + 3·0 + 1
n = 1: 23 = 13 + 3·12 + 3·1 + 1
n = 2: 33 = 23 + 3·22 + 3·2 + 1
n = 3: 43 = 33 + 3·32 + 3·3 + 1
······
n = n: (n+1)3 = n2 + 3·n2 + 3·n + 1
Sumando y simplificando los cubos:
(n+1)3 = 3·(12 + 22 + 32 + ··· + n2 )+ 3·(1+2+3+···+n) + n + 1
3·(12 + 22 + 32 + ··· + n2 ) = (n+1)3 – 3·(1+2+3+···+n) – (n + 1)
3·(12 + 22 + 32 + ··· + n2 ) = (n+1)3 – 3·n(n+1)/2– (n + 1)
3·(12 + 22 + 32 + ··· + n2 ) = (n+1) [(n+1)2 – 3·n/2 – 1]
3·(12 + 22 + 32 + ··· + n2 ) = (n+1) [(n+2n)·n– 3·n/2]
3·(12 + 22 + 32 + ··· + n2 ) = (n+1) [(2n2+n) /2]
3·(12 + 22 + 32 + ··· + n2 ) = 1/2(n(2n+1)(n+1)
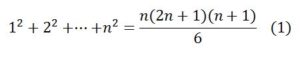
El mismo procedimiento se podría aplicar para calcular la suma de los cubos de los n primeros números naturales partir del desarrollo de (n+1)4= n4 + 4n3 + 6n2 + 4n + 1 dando valores sucesivos a n, obtendríamos:
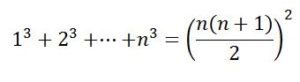
NÚMEROS PIRAMIDALES
Un número piramidal de base cuadrada es un número figurado que se obtiene apilando esferas iguales. Si la base de la pirámide tiene n esferas de lado, la capa superior será un cuadrado de n-1 esferas de lado, la siguiente capa será un cuadrado de n-2 esferas de lado y así sucesivamente.
Ejercicio 1.- Calcular el número de bolas que se pueden apilar en forma de pirámide de base cuadrada cuyo lado de la tiene 8 bolas

Solución: Aplicando la fórmula (1)
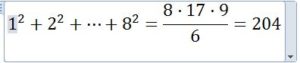
Ejercicio 2.- Calcular la suma de los cuadrados de los ocho primeros múltiplos de siete
Solución: S = 72 + 142 + 212 + ··· + 562 = 72( 12 + 22 + 32 ··· + 82) = 49·204 = 9996
Ejercicio 3.- Calcular el número de bolas que se pueden colocar en una pirámide de base triángulo equilátero de n bolas de lado.
Solución: El triángulo de la base contiene n + (n-1) + (n-2) + … + 2 + 1 = (n2+n)/2 bolas. La suma de las bolas de los n triángulos que forman la pirámide será:
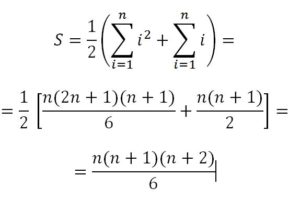
Ejercicio 4.- Calcular el número de bolas que se pueden apilar en una pirámide de base rectangular de dimensiones nxm
Solución: Sea m el número de bolas del lado mayor de la base y n en número de bolas en el lado menor.
En la capa superior habrá una fila de bolas de longitud m-(n-1) = m-n+1
En la siguiente habrá dos filas cada una de ellas con una unidad más de longitud que las de la capa anterior 2·(m-n+2)
En la siguiente habrá tres filas cada una de ellas con una con unidad más de longitud que las de la capa anterior 3·(m-n+3)
En la siguiente habrá cuatro filas cada una de ellas con una con unidad más de longitud que las de la capa anterior 4·(m-n+4)
En la base el número es n·(m-n+n) = n·m
Sumando las bolas de todas las capas:
(m-n+1) + 2·(m-n+2) + 3·(m-n+3) + … + n·(m-n+n) =
= (m-n) + 1 + 2·(m-n) + 22 + 3·(m-n) + 32 + … + n·(m-n) + n2 =
= (m-n)·(1+ 2 + 3 + …+ n) + 12 + 22 + 32 + ··· + n2 =