La matemática griega alcanzó un nivel extraordinario en Geometría, pero tenía algunas limitaciones que influyeron en el desarrollo posterior de las matemáticas. El descubrimiento de los números irracionales en la Escuela Pitagórica significó un serio obstáculo para el desarrollo de la Aritmética y del Algebra. Además, el descubrimiento supuso una vuelta a la Geometría como rama preferente de la Matemáticas Griega. Dejando la Aritmética y refugiándose en la Geometria se evitaba un encuentro directo con los irracionales. Esta decisión los llevó a distinguir entre número y magnitud
Diofanto de Alejandría (siglo III) introdujo el simbolismo en Algebra: 𝜁 como x, Dg como x2, Kg como x3, DgD como x4, KgK como x6. Esta notación tiene gran importancia porque hay potencias superiores a tres que no tienen sentido en la Geometría y si lo adquiere bajo supuestos aritméticos que es precisamente el punto de partida de Diofanto. La ejecución de las operaciones es completamente aritmética sin hacer ninguna referencia a la Geometría que le pudiera servir de apoyo o justificación.
Diofanto demostró en su Aritmética una gran habilidad para reducir los problemas a ecuaciones o situaciones que pudiera manejar, aunque no decía el camino que había seguido para lograr tales reducciones. Morris Klein sugiere que emplearía el Algebra Geométrica recogida en el libro II de los Elementos de Euclides, aunque éste nunca resolvió problemas indeterminados como los planteados por Diofanto.
Lo cierto es que los problemas que planteó y resolvió Diofanto eran distintos a los que se habían planteado sus predecesores, pero no tenía ningún método general para resolverlos y aún teniendo su Aritmética más de 50 tipos de problemas no intentó clasificarlos. Diofanto ha sido considerado por esa notación y por los problemas que resolvió como precursor del Álgebra. La metodología para la resolución de problemas no era uniforme y los métodos de Diofanto proceden de una mente genial y creativa y no de unos métodos generales que establecería el álgebra en el futuro. La notación algebraica de Diofanto se conoce como sincopada

La expansión del Imperio árabe puso en contacto, a través de la Casa de la Sabiduría de Bagdad, la geometría griega, recogida en el mundo griego y sobre todo en los libros de la biblioteca de Alejandría, con la aritmética hindú con sistema de numeración posicional y basada en las diez cifras. Al-Khwarizmi (780-850) expuso un álgebra puramente retórica sin fórmulas ni simplificaciones para facilitar las operaciones que se presentan para afrontar las necesidades de la cada diario sin ningún otro fin superior.
Un cuadrado y diez de sus raíces son iguales a 39 unidades, es decir que si sumamos 10 raíces a un cuadrado su suma es igual a 39 unidades.
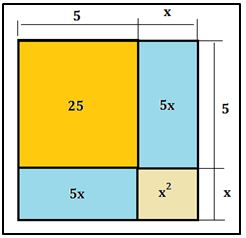
Da la solución así : Tomemos la mitad del número de raíces, esto es 5, y multipliquemos esta cantidad por si misma y el resultado es 25. Añadamos a 39 lo que da 64 (es decir 25) hagamos su raíz cuadrada, ocho, y restemos la mitad del número de raíces , precisamente 3, esta es la solución. Equivale a completar cuadrados
Tabit ibn Qurra (836-901) resolvió ecuaciones de tercer grado por consideraciones geométricas, que no conducían a resultados numéricos.
La trigonometría, que desarrollaron para los estudios astronómicos, fue una motivación para el desarrollo del Álgebra se disponía de las tablas de Claudio Ptolomeo (100-170) y las del astrónomo indio Aryabhata (476-550). Intentando calcular el seno de un grado con la mayor precisión posible se estudiaron relaciones entre las diferentes que se convirtieron en una fuente constante expresiones y relaciones algebraicas.
En el siglo XIII, Jordano Nemorarius (1225-1260). escribió una Aritmética de orientación bien distinta a Liber Abaci en la cual utilizaba letras para representar un número cualquiera. Para demostrar que si un número se divide en dos partes de manera que su producto es conocido ambas partes están determinadas rezona así:
“Sea abc un número dado y sean ab y c las partes en que está dividido, sea d el producto definido de las dos partes ab y c, Sea e el cuadrado de abc y sea f cuatro veces d, y sea g el resultado de sacar f de e. Entonces g es el cuadrado de la diferencia entre ab y c. Sea h la raíz cuadrada de g. Entonces h es la diferencia entre ab y c. Desde que h es conocida, entonces c y ab están determinados
También Th. Bradwardino (1300-1349) utilizó un álgebra retórica para expresar relaciones funcionales, pero utilizó letras en vez de números para expresar las cantidades variables o para designar una cantidad en general. Las operaciones de adición, sustracción, multiplicación que se realizaban entre las cantidades las describe con palabras sin utilizar simbología formal alguna.
Siguiendo la línea de Al-Khwarizmi surgieron en el mundo occidental una serie de álgebras Le Triparty en la science des nombres (1484) de N. Chuquet (1445-1500) fue el libro que, tanto por el nivel de su tratamiento como por la importancia de sus ideas es el más importante desde Liber Abaci (1202) de Fibonacci.

El álgebra retórica alcanzó su culminación con la publicación de Ars magna de G. Cardano (1501-1576), donde se daban las reglas de la resolución de la ecuaciones de tercer y cuarto grado. Da la fórmula de resolución de la cúbica x3 + ax = N de la siguiente forma:
Eleve al cubo un tercio del número de las cosas (a) sumadle a esto, el cuadrado de la mitad del número de la ecuación (N) y haced la raíz cuadrada de todo. Pondrá esto dos veces, y a una de las dos sumar una mitad del número del que habías elevado al cuadrado y del otro, restad la mitad del mismo. Tendréis entonces tendrá entonces un binomio y su epítome. Entonces substrae la raíz cúbica del epítome de la raíz cúbica del binomio, el residuo es el lado buscado.
En lenguaje simbólico este retoricismo se expresaría así:
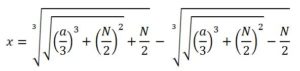
Luca Pacioli había comparado en dificultad la resolución de la cúbica con el problema de la cuadratura del círculo. El éxito de esta obra eclipsó los éxitos pequeños, pero imprescindibles de los otros algebristas. Pero el lenguaje no estaba elaborado las soluciones se expresaban en lenguaje ordinario resultaba farragoso y era poco operativo. El logro de los algebristas italianos supone la culminación del álgebra retórica.
El avance en la notación algebraica fue una obra coral y dilatada en el tiempo y formaron parte del proceso una serie de matemáticos que han quedado relegados a un segundo plano frente al éxito logrado por los algebristas italianos a mediados del siglo XVI.
F. Vieta (1540-1603) observó que era necesario encontrar un enfoque general de solución que pasaba por considerarlas en la forma más general posible con coeficientes literales. En segundo lugar había que conjugar la efectividad de los métodos algebraicos con el rigor de las construcciones geométricas que representaban el modelo de rigor científico. Era preciso elaborar una notación que permitiera representar cualquier ecuación. Vieta propuso utilizar vocales para representar lo que se supone desconocido y consonantes para las desconocidas. De esta forma hizo la importante distinción entre parámetro e incógnita.

Con Vieta las letras podían representar números, pero, según él mismo pueden representar a cualquier otra magnitud o especie, es por lo que a este nuevo cálculo que no se basaba en números se llama Álgebra Speciosa, para distinguirlo del cálculo de Diofanto al que denomina logística numerosa, ya sólo se ocupaba de cálculo con números.
Había que dar sentido al cálculo con letras ¿qué significado tienen las potencias A, A2, A3, A4, A5, … ? A representa una longitud, A2, el área de un cuadrado de lado A, y lo llamó cuadrado o plano, A3, representaba el volumen de un cubo de lado A, y lo denominó cubo o sólido. Es evidente que con A4 y A5, se perdía el sentido geométrico, pero lo llamó cuadrado-cuadrado y cuadrado-cubo respectivamente. Igualmente, el sentido podía tener el producto A x E era el área de un rectángulo de lados A y E y producto A x E sería una magnitud plana si A y E fueran lineales. Por otra parte parecía que 6A tenía que representar una longitud seis veces mayor que A, pero, para dar sentido a expresiones como manteniendo la homogeneidad y la concordancia con la geometría fue necesario dotar a los números de dimensión
sólido sólido, por lo tanto. 2 (lineal) 6 sólido
Eran muchos siglos de dominio de la geometría. A la vez que álgebra árabe se iba introduciendo en Europa a través de Italia y España, en muchas ciudades alemanas se publicaban una serie de aritméticas y álgebras, rigurosas y originales y que tuvieron una gran difusión, hasta el punto que en todo Europa se impuso la palabra alemana coss = cosa, para designar la incógnita, y el álgebra se llamó el arte de la coss. Por otra parte J. Widman (1460-) en una aritmética comercial Rechennung auff allen Kauffmanschafft (1489). sustituyó los símbolos p y m, derivados de plus y minus por + y – , símbolos que se utilizaban para designar el exceso o falta de mercancías. Se sabe por Boyer, que Widman conoció el Álgebra de Al-Khowarizmi y que la obra era también conocida por otros matemáticos alemanes.

Otra álgebra alemana fue escrita en 1524 por Adam Riese (1492-1559) que escribió Die Coss, obra de gran difusión, precisión y prestigio, hasta el punto que en Alemania todavía se utiliza la frase nach Adam Riese, como elogio de la exactitud de los cálculos aritméticos. La aritmética de Ch. Rudolff (1500-1545) Coss (1525), empleó las fracciones decimales; la de P. Apian (1495-1552) Rechnung (1527) aparece el triángulo de Pascal.
M. Stifel (1487-1567), escribió la Aritmética integra (1544), que es la más importante álgebra alemana del siglo XVI, incluye el triángulo de Pascal, pero sobre todo destaca en el uso del cálculo con números negativos y el cálculo de raíces y potencias. Extendió las potencias a potencias de exponentes negativos. En la Aritmética integra se usan por primera vez coeficientes negativos, lo que le permitió reducir el número de casos que había que considerar en la resolución de ecuaciones de segundo grado. Y, aunque tenía que explicar cuando usar el signo más o menos en los coeficientes, no admitía los números negativos como soluciones de una ecuación (los llamaba números absurdos) y la variable y las sucesivas potencias de la variable las siguió llamando coss, census, cubus y censicensus, etc. siguó mejorando la notación y en su obra De algorithmi numerorum cossicorum utilizó una sola letra para representar la variable (coss) y las potencias las representa repitiendo la letra de la variable tantas veces como indica el exponente. Este sistema sería adoptado por T. Harriot (1560-1621).

Resumiendo en los años que van desde 1484, fecha de publicación de Le Triparty en la science des nombres de N. Chuquet a 1550 el Algebra se constituye como una rama nueva autónoma de las matemáticas independiente de la geometría. Es claramente la primera corriente de ideas científicas que acabaría cristalizando en la revolución científica, que tenía como objeto fundamental conseguir una naturaleza expresada en lenguaje matemático.
Entre algunos matemáticos aparecía un cierto recelo con el cálculo algebraico, porque aparecía soliciones negativas y sobre todo complejas que carecían de sentido. Con los algoritmos de resolución de ecuaciones, en ocasiones, proporcionaban soluciones que en la geometría carecían de sentido, aparecían soluciones inesperadas, pero la mayor parte de los matemáticos se encontraban a gusto en este terreno. Esta situación la acabó recogiendo J. Le Rond d’Alembert (1717-1783) con su famosa frase: El álgebra es generosa; a menudo da más de lo que se le pide.