
Una vez visto cómo se ha perfilado la idea de función, veamos cómo se llega la noción rigurosa de función continua. En realidad, las ideas dominantes sobre el concepto de función eran, por una parte, la idea de Newton que consideraba que una curva (que se asociaba a la gráfica de una función) estaba engendrada por el movimiento continuo de un punto y que, por lo tanto, se podía dibujar sin levantar el lápiz del papel. Y, por otra parte, desde L. Euler (1707-1783), la noción de función se asociaba con una sola expresión analítica. Pero la resolución de ecuaciones en derivadas parciales, como sucedió en el caso de la ecuación de la cuerda vibrante estudiada por J. d’Alembert (1717-1783) permitió ampliar el concepto de función a otras funciones con un punto anguloso como el que se produce tensando la cuerda de una guitarra desde un punto. Precisamente el problema de la cuerda vibrante permitió que se pudieran admitir funciones que tuvieran expresiones analíticas diferentes en distintas partes del dominio, lo que permitía que se pudieran admitir funciones discontinuas como:
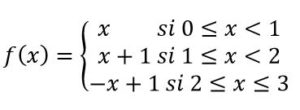
Definida en el intervalo [0,3] que discontinua en x = 1 y x = 2
P.G.L. Dirichlet (1805-1858), apoyándose en la distribución densa de los racionales en el conjunto de los números reales, definió una función f(x), definida en los reales tal que a cada número racional (Q) le corresponde 1 y a los irracionales 0.
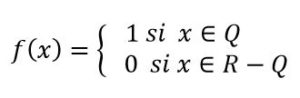
Esta función definida de R no era no era continua para ningún x perteneciente a R.
La noción de continuidad, dada de forma rigurosa y que alcanzó gran difusión entre los matemáticos fue la dada fue por A. Cauchy (1789-1857) en su libro Curso de Análisis (1821). Cauchy definió con precisión el concepto de límite de una función y el de continuidad. Tambíen evitó las críticas a los infinitésimos (como las formuladas por G. Berkeley (1685-1753) considerándolos como variables con límite cero, así como y juntificar los infinitamente grandes como cuyo valor crece más allá de toda cota.
Su definición de continuidad es la siguiente: “f(x) es continua en un punto x = a si un incremento infinitesimal de la variable produce un incremento infinitesimal de la función»; esto es, f(x) es continua en a si:
![]()
Una definición análoga dio B. Bolzano (1781-1848) en 1817 escribía:
La función f(x) es continua en un intervalo si, para cada valor de x en ese intervalo, la diferencia f(x + d) – f(x) se puede hacer tan pequeña como se quiera, tomando d suficientemente pequeño. La definición de Bolzano era análoga a la dada por Cauchy, y algunos historiadores de las matemáticas afirman que Cauchy la conocía, pero lo cierto es que la obra de Bolzano no tuvo la difusión necesaria entre sus contemporáneos y su influencia fue escasa. El trabajo que alcanzó una influencia decisiva fue el Curso de Análisis de Cauchy.
La definición de Cauchy todavía permitía una explicación intuitiva en términos de movimiento cuando decía que una variable es una magnitud que va tomando sucesivamente muchos valores diferentes. En esta definición se observa la presencia de las ideas “temporales» de fluxiones de Newton.
Finalmente, K. Weierstrass (1815-1897) fue el que eliminó del lenguaje del análisis toda relación con el movimiento. Suprimió expresiones como una variable que tiende a un límite (acercándose en el tiempo), y las transformó en desigualdades aritméticas, evitando que, bajo sus expresiones pudiera deslizar la idea de movimiento y cualquier alusión temporal. De él es la definición de continuidad que hoy se llama de épsilon, delta ; f(x) continua en un punto p de R
![]()
También probó que una función continua definida en un intervalo real cerrado alcanzaba en él su máximo y su mínimo absolutos, resultado que ya había sido utilizado por Cauchy sin demostración.




