PROBLEMAS DE GEOMETRÍA VISUAL (I)

En este título analizaremos algunos problemas de geometría que se plantean con el soporte de una figura. Para resolverlos bastará con utilizar los principios básicos de la geometría, teoremas sencillos, como el teorema de Pitágoras y el manejo de la noción de semejanza en el plano.

Problema 1. En la figura el cuadrado ABDD está inscrito en una circunferencia de radio R y el cuadrado A’B’C’D’ tiene los vértices A’ y B’ en la circunferencia y el lado C’B’ pasa por el cetro. ¿cuál es la razón de sus áreas?

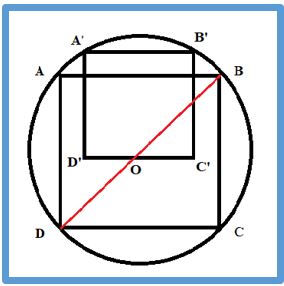
Solución: El área del cuadrado ABCD, inscrito en la circunferencia de radio R. Su diagonal mide 2R  y su área será 4R²/2 = 2R².

El área del cuadrado A’B’C’D’ la calcularemos a partir del triángulo rectángulo A’D’O, cuya hipotenusa mide R.

Cateto A’D’= 2x (lado del cuadrado)

Cateto D’O = x

Hipotenusa OA’ = R

Por el teorema de Pitágoras: (2x)² + x² = R²    ⇒   5 x² = R²       ⇒   x² = R² /5 

El área de A’B’C’D’ será  4x² = 4R²/5

  El cociente de las áreas = 2R² / (4R²/5) = 5/2

Problema 2. Dado el triángulo ABC de lados, 36, 77 y 85 cm

1. Demostrar que es rectángulo.
2. Si P es el punto medio de BC y PQ es perpendicular a la hipotenusa. Calcular el área del cuadrilátero ABPQ
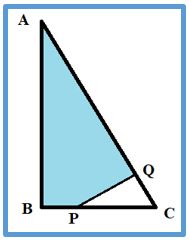4. Solución:
   1. Basta ver que las medidas cumplen el teorema de Pitágoras:

   85² = 36² + 77²          7225 = 1296 + 5929

   1. Los triángulos ABC y PQC con semejantes la razón entre sus hipotenusas será: 85 /18 = 4,72   ⇒    La razón entre sus áreas será:

   4,72² =22,30

   Área del triángulo grande= 1386 cm².  ⇒    Area del pequeño 62,15 cm².

   Problema 3.- Dado el triángulo ABC de lados 39, 80, 89) cm

   1. Demostrar que es rectángulo
   2. Si PB = 2PA y PQ es perpendicular a la hipotenusa. Calcular el área del triángulo PQC
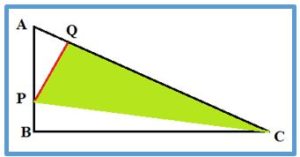   3. Solución:
      1. a) Basta ver que las medidas cumplen el teorema de Pitágoras: 89² = 80² + 39²        7921= 6400 + 1521
      2. b) Area de ABC =39×80/2 =1560 cm².

      Area de PBC = 80×13/2 = 520 cm².    (PB =13 cm)

      Area de AQP; AQP es semejante a ABC, la razón de semejanza entre ellos será  89/26 = 3,42   ⇒ Razón entre áreas 11,72  ⇒   Area de AQP = 1560/11,72 =133,13 cm².

      Por tanto: área PQC = 1560- 520-133,13 = 906,87 cm².

       

      Problema 4.- En la figura ABEH, BCDE y HEFG son cuadrados de lado 2cm, calcula el área de la figura coloreada AOB

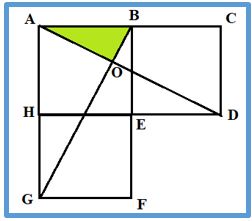       Solución: El triángulo  AOB es semejante a ACD. Razón de semejanza:

      AB/AD = 1/Ö5    ⇒ (la razón entre las áreas es igual al cuadrado de la razón de semejanza)  ⇒  área de AOB/área de ACD  =  1/5

      Como área de ACD = 4   y  ⇒     área de AOB = 4/5

       

   5. Problema 5.– ¿Qué fracción de rectángulo ABCD es el área de la figura coloreada, sabiendo que M es el punto medio de AB, N el punto medio de BC, P el punto medio de CD,  Q el punto medio de AD y O el punto medio de QM.
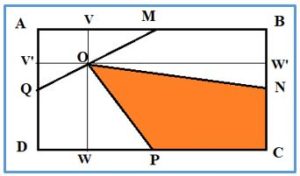   6. Solución: Como AM=MB y AV = VM,  Llamando AV = a, el lado del rectángulo AB = 4aComo AQ =QB y AV’ = V’D,  Llamando AV’ = b, el lado del rectángulo AD = 4b

      Área de la figura OPCN: 3a·3b – 3ab/2-3ab/2 = 9ab-3ab = 6ab

      Área del rectángulo ABCD 4a·4b = 16 ab

      Luego la fracción de rectángulo ABCD que es  el área de la figura QPCN será:  16 ab/6ab = 8/3