Para construir la dinámica moderna hubo que abandonar la idea aristotélica de que la pesantez y la levedad eran cualidades opuestas. Los cuerpos graves o pesados tenían en su naturaleza la necesidad de dirigirse hacia el centro de la Tierra y los cuerpos leves tenían una tendencia interior que les obligaba a alejarse del centro y encaminarse hacia la periferia del mundo sublunar, que mayoritariamente estaría ocupada por el fuego, puesto que era el más leve de los elementos.
Para llegar a definir la gravedad no como una tendencia interna de los cuerpos materiales, sino como una relación entre objetos, sería necesario dejar de estudiar el movimiento en un espacio tal como lo concebían Aristóteles y la mayor parte de los filósofos griegos (salvo los atomistas). Es decir, se necesitaba pasar de un espacio con sus posiciones absolutas, lleno de elementos y sin espacio vacío entre ellos y en el que sólo se consideraban cualidades de los cuerpos a otro espacio abstracto en el que se pudieran expresar las magnitudes medibles, en suma, al espacio abstracto de la geometría euclidiana.
Este paso suponía renunciar a la antigua idea del cosmos finito y ordenado de las esferas homocéntricas, implicaba admitir el vacío y empezar a considerar la existencia de un universo infinito.
Debemos observar que no era fácil salirse de una estructura científica lógicamente establecida y elaborada acorde con nuestra experiencia sensorial como eran la cosmología y la física aristotélicas y admitir que el movimiento era una situación estable de los cuerpos, igual que lo que era el reposo, así como admitir la existencia del vacío y tratar de adaptarse comprender las nuevas evidencias numéricas y observacionales que aportaba el método experimental. Por otra parte, las explicaciones de la física aristotélica no eran fácilmente refutables y debemos tener en cuenta que las explicaciones que aportaba la ciencia aristotélica sobre el conocimiento del mundo tuvieron sentido para mucha gente inteligente durante muchos años.
A la erosión de la cosmología aristotélica contribuyó N. Copérnico(1473-1543) con si publicación de De Revolutionibis (1543) con la que transformó la astronomía, que proponía el sistema heliocéntrico que fue secundado por los astrónomos más notables, en particular por Galileo Galilei (1564-1642) , que, en 1609 aportó el uso telescopio a la observación astronómica. Uno de los grandes descubrimientos de Galileo fue el de los satélites de Júpiter que los llamó satélites mediceos en honor de Cósimo II (1590-1621), Gran Duque de la Toscana del que fue maestro Galileo de 1606 a 1609.
Galileo Galillei realizó descubrimientos revolucionarios que chocaban frontalmente con la física aristotélica, que mantenía que el movimiento natural de los cuerpos era una tendencia natural de los mismos buscando el lugar de reposo permanente que les correspondía según su pesantez o levedad y que el movimiento se realizaba en un espacio lleno en el cual los cuerpos se movían en una especie de “sopa gravitatoria” formada por todos los demás cuerpos. Ante esta situación, mientras estaba en la universidad de Padua tomó la decisión de no aceptar en filosofía más premisas que las que procedieran de la comprobación y de la experiencia. Y desde 1589 Galileo no se limitó a observar y a teorizar sobre las observaciones, sino que dio un paso más, experimentó en diferentes situaciones, algunas de ellas ideales, extrapolaciones del propio proceso experimental.
Empezó a experimentar con planos inclinados, dejando rodar bolas lisas sobre planos inclinados bien pulimentados y pudo observar que, en la pendiente las bolas avanzaban con una aceleración constante y en 1604, descubrió la ley del movimiento uniformemente acelerado y llegó a las siguientes conclusiones:
- Que el movimiento era un estado natural de la materia y que la fuerza para mantener un cuerpo en movimiento solamente se necesitaba cuando había fricción.
- También estableció la ley inercia de los objetos, que dice que en ausencia de fuerzas exteriores todo cuerpo permanecía en movimiento rectilíneo y uniforme, y, entre las fuerzas exteriores, estaba la fricción o fuerza de rozamiento.
- Demostró que el aire que llenaba el espacio ejercía rozamiento sobre los cuerpos, los frenaba. Y postuló que una bala de cañón y una pluma, dejadas caer libremente desde una misma altura, llegarían al suelo a la vez si no existiera la resistencia del aire.
- Con esos supuestos concluyó que todos los cuerpos caerían con igual velocidad en el espacio vacío y comenzó a realizar experimentos en los que el rozamiento, ya fuera de la superficie de deslizamiento o del aire, tuvieran poca influencia. (Utilizando lubricantes para minimizar el rozamiento, dejar caer en el aire cuerpos de elevada densidad, etc, etc).
Galileo realizó una notable abstracción de la realidad estudiando una característica (distancia, velocidad tiempo empleado) del movimiento en el vacío a partir de unos principios experimentales plausibles y cuyos resultados se podían medir, con lo que superaba el carácter cualitativo de la física aristotélica. Luego, para estudiar el movimiento real de forma completa, se debía considerar el efecto de las fuerzas de fricción para completar el movimiento real de los cuerpos.
Con sus observaciones, Galileo descubrió que la fricción era la fuerza que detenía el movimiento de un cuerpo y no las cualidades de levedad o de pesantez que tenía cada cuerpo, como afirmaba Aristóteles.
No obstante, cuando en 1638, escribió su última obra Discursos sobre dos nuevas ciencias, donde estableció los fundamentos de la dinámica como ciencia y se suele considerar como el fin de la física aristotélica, el propio Galileo mantenía el vocabulario, e incluso ideas, de la física aristotélica cuando en la jornada tercera de la obra, dice por boca de Salviati:
“Un cuerpo grave posee, por naturaleza, la propiedad intrínseca de dirigirse hacia el centro común de gravedad, o sea, hacia el centro de nuestro globo terrestre, con movimiento constante y uniformemente acelerado; es decir, que en tiempos iguales se hacen adiciones iguales de nuevos incrementos de velocidad”.
Y luego matiza que eso se verifica en el vacío:
“Es cierto que esta aceleración uniforme puede modificarse por la resistencia del medio ofrece al cuerpo a atravesarlo y desplazarlo hacia los lados para abrirse paso en su caída… Sin embargo, la resistencia del aire al poco peso del globo es grande mientras que la resistencia a l gran peso de la bola de plomo es muy pequeña, me hace suponer que, si el aire desapareciese del todo, añadiría así inmensas facilidades al avance del globo y muy pocas al avance del plomo y las velocidades globo y la bola de plomo llegarían a igualarse
¿Cuáles fueron las pruebas realizadas por Galileo para estudiar el movimiento? Para eso puede verse: https://vicmat.com/galileo-la-medida-la-aceleracion-gravitatoria-g/
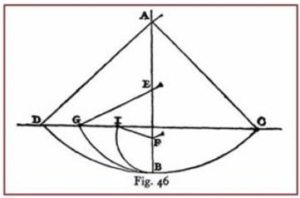
La idea de experimentar con planos inclinados y realizar medidas le vino de la observación de la lámpara de una iglesia. Realizó el experimento en el péndulo y observó que en un péndulo de longitud AB que pendía de A y que en el extremo tenía una bola de plomo B. cuando se le interponía un clavo E en una posición intermedia en la vertical AB, modificando con ello la longitud del péndulo y luego lo probó colocando el clavo en la posición P y en los dos casos, la bola de plomo alcanzaba la misma altura. De lo que dedujo que, en todos los casos, en el punto más bajo de la trayectoria la velocidad de la bola era la misma en ambos sentidos de la oscilación. Por lo tanto, la velocidad de la bola en el punto más bajo no dependía de la longitud del péndulo, sino de la altura de la que partía la oscilación.
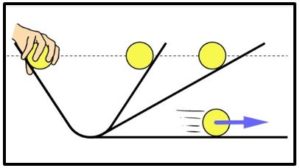
Con esa observación, Galileo vislumbró la similitud entre el péndulo y el plano inclinado y pensó que si una bola rodaba por un plano inclinado encerado y a continuación se encontraba otro plano inclinado hacia arriba y seguía su movimiento, la bola alcanzaría la misma altura que la del punto del que partió, tal y como sucedía con el péndulo y así fue. Por lo tanto, la velocidad con que llegaba al suelo una bola que descendía por un plano inclinado no dependía de la inclinación del plano, sino de la altura vertical de partida.
Con esta estas ideas, Galileo midió la velocidad de caída libre de un cuerpo, partirndo de las siguientes observaciones
Primera: Las velocidades alcanzadas por un mismo móvil, en planos de diferente inclinación, son iguales siempre y cuando las alturas de los mismos planos sean iguales.
Segunda: Con la observación anterior bastaba que midiera la velocidad la tarea de medir la velocidad de caída libre de un cuerpo se podía hacer midiendo la velocidad de caída por un plano inclinado de poca pendiente que sería la misma que la de la caída libre.
Tercera: Midiendo las distancias recorridas en un plano inclinado por una bola desde la parte más alta, observó que en el primer intervalo de tiempo recorría una distancia L, en el segundo intervalo 3L, en tercero 5L, en el cuarto 7L, en el enésimo (2n-1) L. De donde obtuvo las siguientes conclusiones: (supondremos L lo expresamos en centímetros y que cada intervalo de tiempo es un segundo)
Conclusión 1.– El movimiento era uniformemente acelerado ya que el espacio recorrido cada segundo (la velocidad) aumentaba 2L cm/s, luego la aceleración era de 2L cm/s2.
Conclusión 2.- Galileo dedujo que la velocidad el movimiento uniformemente acelerado era proporcional al tiempo: vt = a·t. Como la aceleración a = 2L. Si en el instante inicial v0 = 0 y al cabo de t segundos vt se tiene que vt – v0 = a·t ⇒ vt = a·t.
Conclusión 3.- El espacio s recorrido en t segundos era proporcional a t2, como se puede comprobar realizando la suma de la siguiente progresión aritmética:
s = L + 3L + 5L + 7L + ···+ (2t-1) L = [1 + 3 + 5 + 7+ ··· + (2t-1)] L = t2·L,
Como la aceleración a = 2L, se obtiene: s = a·t2/2
Por tanto, la distancia total recorrida durante cierto período de tiempo era proporcional al cuadrado de este tiempo
Conclusión 4.- Cuanto más inclinado estaba el plano, mayores era las distancias recorridas, pero sus relaciones seguían siendo las mismas. Galileo, concluyó que esas relaciones debían verificarse también cuando el ángulo α = 90º, esto es, para la caída vertical.
Calculó la aceleración constante g. Con plano con un ángulo de inclinación α respecto a la horizontal y obtuvo la relación:
![]()
donde a era la aceleración con la cual descendía la bola por el plano inclinado.