Dos problemas clásicos que aparecen en muchos libros de Matemática Recreativa en los que, aparentemente, hay que romper las unidades que se desean repartir.
PROBLEMA 1: Tres náufragos llegan a una isla y se encuentran un montón de cocos. Deciden repartirlos entre los tres, pero era tarde dejaron el reparto para el día siguiente. Durante la noche el primer náufrago se despertó y retiró la mitad de los cocos más medio coco y se volvió a dormir. Después se despertó el segundo náufrago que se hizo acopio para él la mitad de los cocos que quedaban más medio coco y se acostó. A continuación, el tercer náufrago se apropió de la mitad de los cocos que quedaban y medio coco. Al amanecer se reúnen para hacer el reparto de los cocos (que habían quedado) en tres partes iguales regalando un coco que sobraba un mono que había en la isla ¿Cuántos cocos había como mínimo en el montón inicial y cuántos se llevó cada uno?
Solución: Supongamos que hay N cocos en el montón:
El primero se lleva N/2 + 1/2 = (N + 1)/2 por lo tanto quedan: (N – 1)/2 cocos.
El segundo se lleva (N – 1)/4 +1/2 = (N + 1)/4 por lo que quedan: (N – 3)/4 cocos
El tercero se lleva (N – 3)/8 + 1/2 = (N + 1)/8 y queda un coco, por lo que
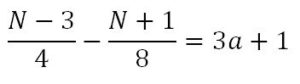
Siendo a el número de cocos que se lleva cada uno en el reparto del amanecer
De donde 2(N – 3) – (N +1) = 8 (3a +1) ⇒ N = 15 + 24 a
El número mínimo de cocos se obtiene para a = 1, que da N = 15. Se puede comprobar que el resultado es correcto:
Con 15 cocos el primero se lleva la mitad más medio coco, es decir, 8 (7,5+ 0,5 = 8) y quedan 7 coco
El segundo se lleva la mitad de 7 más medio coco, esto es, 4 cocos (3,5 + 0,5 = 4) y quedan 3.
El tercero se lleva la mitad de 3 más medio coco, 2 (1,5 + 0,5 =, 2) cocos y queda un coco para el mono.
PROBLEMA 2: Un jeque dejó a sus hijas cierto número de perlas y dispuso que se las repartieran de la siguiente manera: a la hija mayor le correspondería una perla más un séptimo de las restantes; a la segunda, dos perlas más un séptimo de las restantes; a la tercera, tres perlas más un séptimo de las restantes, y así sucesivamente hasta la hija más pequeña. Alguna de las hijas recurrió a un juez alegando alegando que con ese reparto salían perjudicadas respecto a sus hermanas. Pero el juez, que era hábil en aritmética de repartos, les dijo que la división propuesta por su padre era equitativa y que realizaran el reparto. Tras efectuar el reparto todas las hermanas recibieron el mismo número de perlas. ¿Cuántas hijas tenía el jeque y cuántas perlas se repartieron?
Solución: Las condiciones que se consideran son que la perlas no se parten, por lo tanto, como a hija mayor recibe una perla más un séptimo del resto N – 1 debe ser múltiplo de siete.
El problema se puede resolver analíticamente igualando la cantidad de perlas que recibe la hija mayor con la que recibe la segunda. Si N el número de perlas de la herencia. La hija mayor recibe 1 perla más 1/7 de las restantes, es decir:
Quedan entonces:
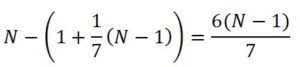La segunda hija toma dos perlas más 1/7 del resto, es decir,
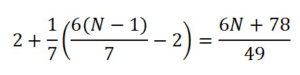Igualando ambas expresiones y resolviendo la ecuación:
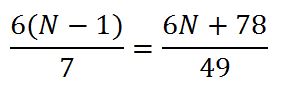
se obtiene que : N = 36 perlas.
La primera obtuvo en el reparto una perla y, además, un séptimo de 35, luego logró 6 perlas y dejó 30 perlas.
La segunda, de las 30 que encontró obtuvo 2 y, además, un séptimo de 28, luego, sacó 6 y dejó 24 perlas.
La tercera, de las 24 que encontró, consiguió 3 más un séptimo de 21, o sea 3, en total seis perlas y dejó 18 perlas.
La cuarta, de las 18 que encontró, logró 4 perlas más la séptima parte de 14, o sea 2 y recibió, 6 perlas y dejó 12 perlas.
La quinta hija encontró 12 perlas; le correspondieron 5 más un séptimo de 7, luego sacó 6.
A la hija más joven le correspondieron, por fin, las 6 perlas restantes más un séptimo de cero.
En el libro El hombre que calculaba de Malba Tahan se expone otro problema, el de los tres marineros, similar al del mono y los cocos; tan similar que probablemente sea su antecedente directo. Lo expongo sin solución razonada, pero se da el resultado:
PROBLEMA 3: Tres marineros reciben como recompensa un montón de monedas que han de repartirse al día siguiente. Por la noche, uno de los marineros se despierta, divide las monedas en tres partes iguales, tira al mar una moneda que sobra y se lleva su parte. El segundo y el tercer marinero, sucesivamente, hacen lo mismo. A la mañana siguiente el capitán divide las monedas restantes en tres partes iguales, se queda una moneda que sobra y le da una parte a cada marinero. ¿Cuántas monedas había?
Sol 241.
