
El conjunto de Cantor fue descrito dado a conocer en 1883 por el matemático G. Cantor (1845-1918). Este conjunto había sido estudiado en 1875 por el matemático irlandés, Henry J. S. Smith (1826-1883), pero su descubrimiento no fue conocido hasta la publicación del matemático alemán
El conjunto de Cantor se coloca hoy entre los conjuntos fractales, pero, en el momento de su aparición, se le clasificó en la galería de monstruos matemáticos, era un conjunto paradójico, que no pasaba de ser un objeto, construido por matemáticos juguetones, que presentaba propiedades curiosas, pero que era un sinsentido que carecía de aplicaciones en el mundo real.
Entre las propiedades extrañas del conjunto de Cantor destacaremos la siguiente: Es un conjunto no numerable contenido en el intervalo real [0,1] que tiene longitud cero y posee tantos elementos como el intervalo real [0,1] entero.
Entre las inesperadas aplicaciones del mismo diremos que B. Mandelbrot (1924-2010) lo utilizó en 1962 como modelo aproximado para describir las ráfagas de errores en las líneas de transmisiones de datos en dispositivos informáticos.
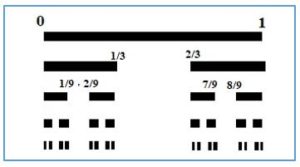
Comenzaremos por definir el conjunto de Cantor de forma geométrica, para ello tomaremos del intervalo cerrado de los números reales [0,1], que lo dividiremos en tres partes iguales y eliminamos el intervalo abierto central, esto es, el intervalo eliminamos (1/3, 2/3). Con cada uno de los segmentos cerrados restantes se repite el proceso indefinidamente, Los puntos que quedan en ese proceso indefinido es el conjunto de Cantor, K, tal como sugiere la figura.
El proceso es como sigue:
Intervalo de partida (orden 0) : E0 = [0,1]
Paso 1 (orden 1): E11 = [0, 1/3], E12 = [2/3, 1]
E1 = E11 ꓴ E12
Paso 2 (orden 2): E21 = [0,1/9], E22 = [2/9, 3/9], E23 = [6/9,7/9], E24 = [8/9 , 1]
E2 = E21 ꓴ E22 ꓴ E23 ꓴ E24
Es evidente que, en cada paso, se duplica el número de intervalos y se divide entre tres la longitud de cada uno de ellos. Continuando este proceso n pasos llegamos a un conjunto En (de orden n) formado por 2n segmentos de longitud 3-n y es claro que: Debemos observar que En ⸦ En-1 y que el conjunto limite en infinitos pasos será el conjunto K de Cantor;
Debemos observar que En ⸦ En-1 y que el conjunto limite en infinitos pasos será el conjunto K de Cantor;
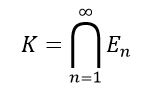
Las propiedades K son extrañas:
Propiedad 1.- El conjunto de Cantor K es no vacío, porque, por lo menos, contiene los extremos de los intervalos que lo generan.
Propiedad 2.- K es totalmente inconexo. Es decir los puntos están totalmente disociados, es por lo que a K se le llama también polvo de Cantor
Es fácil ver Dos puntos P y Q no pueden pertenecer un intervalo de longitud 3-n pues siempre habría un intervalo 3-m tal que 3-m < |P – Q|, lo que garantiza que los puntos intermedios no pertenecen Em y, por lo tanto, a K.
Propiedad 3.- Aunque tiene infinitos puntos su longitud es nula.
Podemos calcular si, restando a la longitud del intervalo de los números reales [0,1], que es 1, las longitudes que le quitamos en cada paso ¿Qué longitud le quitamos a [0,1]?

En total quitamos:

Por lo que la longitud de K es 0
También podríamos calcular la longitud partiendo de la fórmula
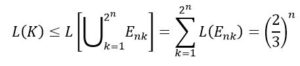
Siendo n tan grande como se desee, por tanto:

Propiedad 4. K tiene tantos elementos como el intervalo real [0,1] , aunque K es totalmente inconexo y [0,1] es un continuo.
Aunque su longitud es nula, ambos conjuntos , K y [0,1], son dos conjuntos coordinables ya que existe una biyección f de K en [0,1]
Una idea de la demostración es la siguiente: Como el K ⸦ [0,1] como mucho, K tendrá tantos puntos como él. Vamos a comprobar que, ambos tienen la misma cantidad de puntos, para ello construiremos aplicación suprayectiva de K en [0,1], es decir, una aplicación que a cada punto de K le haga corresponder otro punto de [0,1]. de forma que cada punto de [0,1] sean imagen de, al menos un punto de K.
La aplicación la construimos así: seleccionamos un pinto P de K. En el primer paso de la construcción de K P estará contenido en uno de los dos subintervalo de [0,1]: K0 (el de la izquierda) o K1 (el de la derecha), supongamos que está en K0 En el segundo paso P estará K00 (subintervalo izquierdo de K0) o en K01 (subintervalo derecho de K0) (supongamos ahora que en K01 en el tercer paso estará en K010 o K011 . Puede observarse que encada paso en cada paso se le añade al intervalo un 0 o un 1, por lo que podemos concluir que el punto P determina de forma única una sucesión de ceros y unos.
Pues bien, a ese punto P del conjunto de Cantor K le hacemos corresponder el número decimal binario 0,010… que sigue el camino de los subintervalos en los que P está contenido
Como cualquier punto del intervalo [0,1] se puede expresar como decimal binario se concluye el esbozo de la demostración
DIMENSIÓN: En cada pas sucesivo hay dos copias escala 1/3 del amnterior, por tanto:

Ese conjunto tendrá medida no nula en esa dimensión recordemos que medido en dimensión 1 su medida es cero
PROPIEDAD EXTRAÑA: K + K = [0,1]
Sin embargo,este conjunto tan extraño, producto de la la pura especulación matemática fue reconocido en el mundo real por B. Mandelbrot al analizar la distorsión que producía un ruido espontáneo en un canal de transmisión de datos. Pero este particular lo analizaremos proximamente.
Víctor Arenzana Hernández




