Los dos ejercicios de optimización siguientes presentas algunas curiosidades. El primero (del camino mínimo) se puede realizar sin hacer uso del Cálculo Infinitesimal recurriendo a las propiedades de la reflexión óptica y el segundo que, dependiendo de los datos, el mínimo relativo que se obtiene con el Cálculo Infinitesimal puede no ser la solución del problema.
Problema 1.- (Camino Mínimo) Dos localidades A y B se encuentran al mismo lado de una autopista recta, de la cual distan 10 km y 20 km, respectivamente. Se desea construir una carretera lo más corta posible, que comunique ambas localidades con un punto de la autopista. Sabiendo que la distancia entre A y B es de 26 km, halla la longitud de la carretera.
Solución: Los plantearemos como un problema de reflexión especular. El gráfico nos ayudará a relacionar los datos y a razonar para resolver el problema, Trataremos de buscar el punto M de la autopista tal que BM + MA se mínimo. Para ello consideremos el punto A’ simétrico de A respecto a la autopista
Observamos que el recorrido ANB tiene la misma longitud que A’NB. Y que este recorrido es mínimo cuando el punto M está a lineado con A’ y B. Por tanto, la distancia mínima es la longitud del segmento A’B, que es la hipotenusa del triángulo rectángulo A’C’B, de catetos: BC’ =30 km y C’A’ = CA
CA es el cateto del triángulo rectángulo ACB y se cumple que
(CA)2 = 262 -102 = 576 ⇒ CA = 24 km
El tiempo mínimo. El siguiente problema puede presentar alguna situación sorprendente, aparentemente paradójica si no tenemos en cuenta que, con los cálculos habituales del Cálculo Infinitesimal, determinamos máximos y mínimos relativos de una función en un intervalo y no extremos absolutos
Problema 2.- Un piragüista está a 6 km de una costa rectilínea. Por el mar alcanza una velocidad de 12 km/h y por tierra a 15 Km/h. Si quiere llegar a un punto Q de la costa que está a una distancia de 10 km del pie de la perpendicular de la recta que va del piragüista a la costa ¿En qué punto de la costa debe desembarcar para que, una vez en tierra, siguiendo por la playa rectilínea, emplee un tiempo mínimo en el recorrido hasta alcanzar el punto Q?
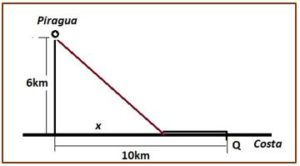
Solución: Si el piragüista desembarca a x km del pie de la perpendicular recorrerá √(36 + x2) km por mar a una velocidad de 12 km/h y (10 – x) km por tierra a una velocidad de 15 km/h, luego el tiempo total hasta llegar a Q, será:
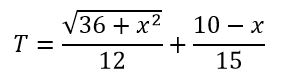
Derivando e igualando T’ = 0 :
Debe desembarcar a 8 km del pue de la perpendicular empleando un tiempo de 54 minutos.
Si el piragüista hubiera estado a 9 km de la playa, el problema se resolvería igual:
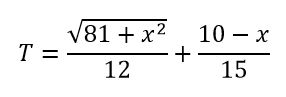Derivando e igualando T’ = 0 :
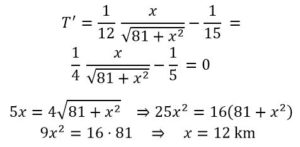
Evidentemente que sobrepasa el punto Q que debe alcanzar y luego retroceder los que es un absurdo. ¿Dónde está el fallo?. [Indicación: El mínimo relativo que se calcula con Cálculo Diferencial cae fuera del intervalo (0, Q) = (0, 10), ya que x = 12. El mínimo relativo caerá en uno de los extremos del intervalo: T(0) =1,42, y T(10) = 1,25, conviene que el piragüista vaya directamente a Q]
