La idea de que la Luna tiene un movimiento de caída permanente hacia la Tierra procede de Newton que comprobó con cálculos que la Fuerza de Gravitación Universal actuaba del mismo modo sobre una manzana que caía del árbol al suelo que sobre la Luna que se movía en su órbita:
Este resultado fue revolucionario y de vital importancia para el pensamiento científico porque durante casi veinte siglos la filosofía aristotélica fue la teoría física dominante y mantenía los cuerpos se movían impulsados por una tendencia interior que les hacía moverse según su naturaleza. En la física aristotélica los cuerpos del mundo sublunar tenían un movimiento natural rectilíneo dirigido hacia el centro de la Tierra y los cuerpos celestes tenían que desplazarse describiendo circunferencias sin necesidad de que actuara sobre ellos fuerza alguna.
Por la Primera Ley del Movimiento, el principio de inercia, Newton consideró que la Luna debía seguir en movimiento rectilíneo y uniforme alejándose de la Tierra si no existiera una fuerza que la desviara de su trayectoria haciéndola girar alrededor de la Tierra, Así, la Luna era atraída hacia la Tierra en el sentido de que descendía por debajo de la línea recta que debía describir si sobre ella no se ejerciera fuerza alguna.
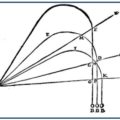
Inspirándose en los estudios de Galileo sobre los lanzamientos horizontales, imaginó que la Luna era un proyectil que giraba alrededor de la Tierra por acción de la gravedad. Newton comparó la Luna con la bala de un cañón que, al ser disparada, debía describir una trayectoria parabólica y, que, aumentando progresivamente la velocidad de lanzamiento, aumentaría su alcance hasta llegar a describir una órbita alrededor de la Tierra.
En el epígrafe tercero de si Sistema del Mundo dice:
“Si consideramos el movimiento de los proyectiles podremos entender que los planetas pueden ser retenidos en ciertas órbitas mediante fuerzas centrípetas; pues una piedra proyectada se va apartando de su camino rectilínea y describe una curva, cuando por la acción de la sola proyección inicial debía haber continuado en línea recta, hasta llegar al suelo.
Aumentando la velocidad de lanzamiento puede ser proyectada cada vez más lejos antes de caer al suelo. Podemos incrementar la velocidad hasta que el proyectil describa un arco de una, dos cinco, diez, cien, mil millas antes de caer, de forma que, al final, supere los límites de la Tierra y pase al espacio sin tocarla…
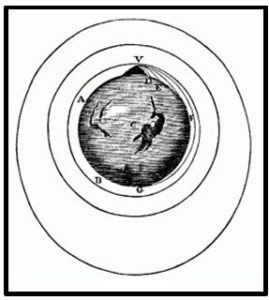
Si, como observamos en la figura, AFB representa la superficie de la Tierra con centro en C y VD, VE y VF se representan las curvas que describiría un cuerpo si fuese lanzado horizontalmente desde la cima de una alta montaña V a más y más velocidad. Debemos pensar, además, que como en los movimientos celestes no existe resistencia al movimiento, para conservar la analogía de los casos, debemos pensar que en la Tierra no hubiera aire, o que, al menos, sea tan sutil que la resistencia sea prácticamente nula.
Entonces, por la misma razón que un cuerpo proyectado con menos velocidad describe el arco menor VD y, proyectado con más velocidad, describe arcos mayores VE, VF y VG, si la velocidad sigue aumentando, el cuerpo acabará llegando más allá de la circunferencia de la Tierra y volviendo a la montaña V desde el que fue lanzado.
Y, puesto que las áreas descritas por el movimiento del radio trazado desde el centro de la Tierra son proporcionales al tiempo que emplean, su velocidad de vuelta a V no será menor que la de lanzamiento, por lo que conservando la misma velocidad, describirá la misma curva una y otra vez, obedeciendo a la misma ley «[Ley de Kepler. Proposición I, Libro I de Principia].
Para Newton, una manzana lanzada horizontalmente y la Luna estaban cayendo, la diferencia era que la Luna tenía un movimiento de caída permanente, mientras que la manzana terminaba su recorrido en superficie terrestre.
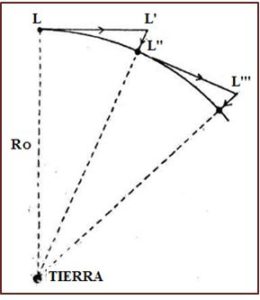
Su razonamiento, en forma algo modificada, se representa en la figura que muestra a la Luna, L girando alrededor de la Tierra, T, en una órbita casi circular. En la posición L, la Luna lleva una velocidad que es perpendicular al radio del círculo.
Si no hubiera fuerzas que actuaran sobre ella, la Luna seguiría una línea recta cumpliendo el Principio de Inercia y, una unidad de tiempo más tarde, estaría en la posición L’. Pero la Luna, siguiendo su órbita circular, llega a la posición de L». Es, precisamente, L’L» la caída libre de la Luna hacia la Tierra. Que es la diferencia de distancias de la Luna al centro de la Tierra entre la posición que debería ocupar si no actuaran fuerzas y la que tiene realmente en la órbita, lo que será.
![]()
Newton probó que la aceleración gravitatoria, g, calculada por Galileo respondía a la misma ley que hacía permanecer a la Luna en su órbita alrededor de la Tierra. La ley no era otra que la Ley de Gravitación Universal, que cumplía la ley del inverso del cuadrado de la distancia.
Galileo había calculado la aceleración gravitatoria para los cuerpos situados en la superficie terrestre, que era de 981 cm/s2. Newton interpretó que esa podía ser la aceleración imprimía la Ley de Gravitación Universal para los cuerpos que se encontraban a una distancia del centro de la Tierra igual a su radio (R = 6.370 km).. Además, Newton sabía que la Luna tenía un periodo orbital de 27 días 7h y 43m y que su órbita, casi circular, tenía 384.400 km de radio y, con estos datos, abordó el problema de calcular numéricamente si la fuerza que atraía a una manzana en la Tierra era la misma que hacía describir a la Luna su órbita.
Primero calculó la caída de la Luna hacia la Tierra en un día, L’L» en la figura. Para ese descenso habrá barrido un ángulo LTL’ de 13º 10’ 35’’ que es el cociente de 360º entre 27,3215 días del periodo orbital de la Luna, se tiene que:
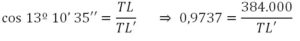
de donde TL’ = 394.381,16, km y la caída diaria de la Luna será LL’ = 10.381,16 km.
Por lo tanto, la Luna cae 10.381,16 km en un día (86.400 segundos).
Newton comprobó si esta caída respondía a un movimiento acelerado tal como lo había calculado Galileo, que satisfacía la ecuación:
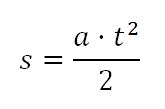
Expresando el espacio en centímetros y el tiempo en segundos:
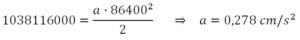
Es una aceleración pequeña, pero, tanto a como g, son aceleraciones que responden a la Ley de Gravitación de Newton en la que las aceleraciones son inversamente proporcionales al cuadrado de la distancia y hemos obtenido que a 6.370 km hay una aceleración de 981 cm/s2 y a 384.000 km una aceleración de 0,278 cm/s2. Se puede comprobar que:
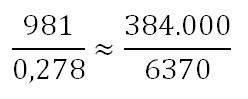
Que son aproximadamente iguales con un error menor del 3%. Cálculos como estos convencieron Newton de que la fuerza de la gravedad terrestre decrecía como el inverso del cuadrado de la distancia al centro de la Tierra y extendió este descubrimiento a todos los cuerpos materiales del Universo, Formulando la Ley de Gravitación Universal según la cual:
Todo cuerpo material atrae a otro con una fuerza directamente proporcional a sus masas e inversamente proporcional al cuadrado de la distancia entre ellos.
El desarrollo de la obra de Newton realizada por los grandes matemáticos de los siglos XVIII y XIX originó una nueva rama de la Astronomía conocida como Mecánica Celeste, que permitió calcular con precisión el movimiento de los planetas del Sistema Solar sometidos la mutua atracción gravitatoria.