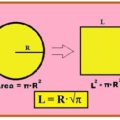
Los griegos consiguieron, con el uso exclusivo de la regla y el compás, cuadrar las áreas de los polígonos. Pero la cuadratura de las figuras limitadas por líneas curvas se les resistieron y recurrieron a otros métodos diferentes; por ejemplo, al método de exhaución, inventado por Eudoxo de Cnido (390-337 a.de C) y utilizado de forma genial por Arquímedes (287-212) para calcular el área de un segmento de parábola. Los griegos se aproximaron al estudio de las cuadraturas figuras limitadas por líneas curvas con el estudio de las lúnulas.
Una lúnula es la superficie limitada entre dos arcos de dos circunferencia (de radios diferentes), que subtienden la misma cuerda, cuando los arcos están situados formando una figura no convexa. Las lúnulas tienen una forma parecida a la que presenta la Luna en cuarto creciente o menguante.
El estudio de las lúnulas de debe al gran geómetra y astrónomo griego Hipócrates de Quíos (470-410 a. C) (no el médico), contemporáneo de Sócrates, que enseñaba matemáticas y escribió unos Elementos de Geometría, anteriores a los Elementos de Euclides (330 – 275 a.C.).
Hipócrates, en su afán de cuadrar figuras limitadas por líneas curvas, demostró que algunos tipos de lúnulas se podían cuadrar, es decir, era posible hallar un cuadrado que tuviera la misma área que ella. Las lúnulas de Hipócrates abrieron el camino de muchos matemáticos para estudiar el problema de la Cuadratura del Círculo, que fue uno de los tres problemas cásicos griegos, junto con la Duplicación del Cubo y la Trisección del Ángulo.
A continuación expondré el cálculo de las áreas de algunas lúnulas y analizaré cuáles son cuadrables en el sentido que le daban los griegos al término:
PRIMERA: Lúnula de triángulo rectángulo isósceles: está limitada por el cuadrante de circunferencia AB trazado con centro en O, y la semicircunferencia AB de dentro el punto meció de la hipotenusa

En la figura se puede observar que:
Llamando OA = OB =c y AB = h, se tiene:
Lúnula + Cuadrante = Triángulo + semicírculo
Lúnula + πc2/4 = Triángulo + π(h/2)2/2
(Por el teorema de Pitágoras: 2c2 = h2)
Lúnula + πc2/4 = Triángulo + (π·2c2/4)/2, por lo tanto:
Lúnula + πc2/4 = Triángulo + πc2/4 ⇒
⇒ Lúnula = Triángulo
SEGUNDA: La Suma de las áreas de las lúnulas sobre un triángulo rectángulo cualquiera es igual al área del triángulo rectángulo. Las lúnulas están limitadas por las semicircunferencias que tienen por diámetros los catetos y la semicircunferencia que tiene por diámetro la hipotenusa.
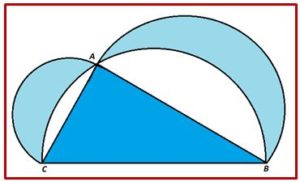
Llamando AC = a, AB = b y CB = c
Lúnulas + semicirculo BC = Triángulo + semicírculo AC + semicírculo AB
Como: semicirculo BC = semicírculo AC + semicírculo AB, por el teorema de pitágoras, se obtiene que:
Lúnulas = Triángulo

TERCERA: La lúnula sobre el lado del cuadrado: Es la lúnula limitada por la circunferencia circunscrita al cuadrado y la semicircunferencia que tiene por diámetro el lado del cuadrado.
Por analogía con el triángulo rectángulo isósceles, tal y como se ha visto en la primera cuadratura de lúnulas. El área de la lúnula sobre el cuadrado es la cuarta parte del cuadrado.
CUARTA: Lúnula sobre el lado del Hexágono (I): Es la lúnula limitada por la circunferencia circunscrita al hexágono y la semicircunferencia que tiene por diámetro el lado del hexágono.
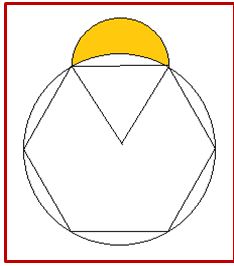
Si el lado del hexágono = 2a, entonces:
Lúnula 1 =
= Semicírculo (r = a) + Triáng. Equilátero (L = 2a) – sector de 60º (r =2a)=
= πa2/2 + a2√3/2 – π·4a2/6 = a2√3/2 – πa2/6 =
= Triáng. equilátero – sector de 60º (r = a)
(multiplicando y dividiendo por 6)
Lúnula 1 = (Área del Hexágono – Área círculo (r =a) )/6 (1)
Luego la lúnula que se obtiene al dibujar una semicircunferencia sobre un lado de un hexágono regular inscrito en una circunferencia es igual a la sexta parte de la diferencia entre el hexágono y un círculo cuyo diámetro es el lado del hexágono (radio = a). Ques esta lúnula sea cuadrable depende de que el círculo sea cuadrable.
Hoy sabemos que esta lúnula no es cuadrable porque depende del área del circulo y en 1882, F. Lindemann (1852-1939) demostró la transcendencia de π lo que implicaba que la cuadratura del círculo es un problema sin solución con los presupuestos de la matemática griega.
QUINTA: Lúnula sobre la diagonal del hexágono (II) Es la lúnula limitada por la circunferencia circunscrita al hexágono y la semicircunferencia que tiene por diámetro la diagonal del mismo.

Si el lado del hexágono = 2a, entonces
Lúnula2 + sector 120º (r=2a) = Triáng. equilátero + Semicírculo (r = a√3)
Por lo tanto:
Lúnula 2 + (π·4a2)/3 = a2√3/2 + π·3a2/2 ⇒
Lúnula 2 = a2√3/2 + π·a2/6
(multiplicando y dividiendo por 6)
Lúnula 2 = (Área del Hexágono + Área círculo (r =a) )/6 (2)
Lúnula 2 tampoco es cuadrable por las mismas razones que Lúnula 1
Sin embargo, la suma de ambas lúnulas (Lúnula 1 y Lúnula 2) si es cuadrable, ya que, observando la figura siguiente y teniendo en cuenta (1) y (2) se tiene:
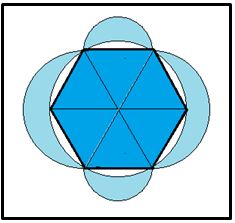
2 (Lúnula 1 + Lúnula 2) = 4 (Área del Hexágono)/6 =
= 2 (Área del Hexágono)/3
Con lo que se prueba que suma de las áreas de cuatro lúnulas de esta figura son las dos terceras partes del área del hexágono. Por lo que la suma de las cuatro lúnulas es cuadrable, no siéndolo ninguno de sus sumandos
Descubrimientos como este despertarían el interés de los matemáticos griegos pare descubrir lúnulas y grupos de lúnulas cuadrables y sobre todo, intentar resolver el problema de la cuadratura del círculo.