
Tradicionalmente las matemáticas han constituido el núcleo de lo que se denominaban Ciencias Exactas. Bajo este epígrafe se reunían todos los estudios de la Física en general y, en particular, la mecánica clásica, la termodinámica, la mecánica cuántica y teorías como la de la relatividad, la del electromagnetismo o la teoría de la información y todas aquellas materias que fueran susceptibles de ser tratadas matemáticamente.
A todas estas ciencias la utilización de las matemáticas les proporcionaba y rigor y una estructura lógica sólida, en principio, irrebatible. Los supuestos y fundamentos de las ciencias asociadas al mundo físico podían estar más o menos ajustados a la realidad, pero se podían contrastar datos experimentales y aceptarlos o refutarlos, pero la teoría matemática que se aplicaba para desarrollar la teoría de esa ciencia debía tener una validez lógica irrefutable.
Por esta razón, cada vez que parecía una paradoja o una contradicción en los conceptos de una teoría matemática pura debía analizarse con lupa y solventarla. En la matemática griega apareció el problema paradójico de la existencia de magnitudes inconmensurables, que, para “solucionarla” (¿sortearla?) se tuvieron que admitir los números irracionales, que eran unos números raros, con infinitos decimales no periódicos, que no se podían representar, que no se habían descubierto y, que además eran más numerosos que los números racionales que se venían manejando hasta entonces, ¿Dónde se había escondido esa multitud?
Podíamos poner muchos ejemplos de paradojas en matemáticas. Es conocida la regla de los signos, pero en aritmética sucede, lo siguiente: (Si tenemos en cuenta que, en aritmética elemental, el cociente de un número entre otro menor es mayor que 1)
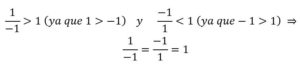
lo que supuso hacer una revisión de las ampliaciones numéricas para fundamentarla lógicamente.
Para trabajar con seguridad en matemáticas y aplicarlas a los estudios de las otras ciencias es preciso manejar teorías matemáticas bien fundamentadas desde el punto de vista lógico, es necesario conocer sus principios y su axiomático deductivo. Esta enseñanza se impartía en las universidades escolásticas desde el siglo XVI . Puede verse la consideración de pons asinorum que tenía para esta enseñanza la proposición 5 del libro I de los Elementos de Euclides. Esta proposición era el ejemplo más utilizado para hacer comprender a los estudiantes la estructura axiomático-deductiva de la geometría euclidiana. Ver el siguiente contacto:
http://vicmat.com/significado-pons-asinorum-la-ensenanza-del-metodo-cientifico/
No obstante, en el aprendizaje de las matemáticas, y para el desarrollo de la creatividad de los estudiantes, es importante analizar demostraciones sin palabras y demostraciones que gráficas y conocer algunas paradojas matemáticas Ver:
http://vicmat.com/la-belleza-las-pruebas-matematicas-las-demostraciones-sin-palabras/
http://vicmat.com/una-demostracion-grafica-la-cuadratura-del-circulo-dejando-lado-la-regla-compas/
Debemos apuntar que en un sistema axiomático –deductivo las condiciones las iniciales, las definiciones y las reglas lógicas de deducción están claramente establecidas y cuando se sale de él se puede caer en contradicciones, paradojas y falacias.
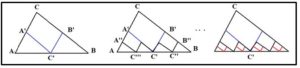
Paradoja 1. En la siguiente figura se “demuestra” que la suma las longitudes de dos lados de un triángulo es igual a la longitud del tercero, esto es que AC + CB = AB. (lo que viene a decir que, entre dos puntos, hay caminos no rectilíneos que también son de mínima distancia)
AB = AC + CB = AA’+ A’C’+ C’B’+ B’B =
= longitud de la línea quebrada de A’’ a B’’, etc. …
Ya que la línea quebrada que pasa por C, paso a paso, se acerca hasta confundirse con el lado AB
Paradoja 2. (La rodadura) Cuando una rueda avanza y da una vuelta completa sin deslizamiento, la distancia que recorre desde que el punto en contacto con el suelo vuelve a estar en contacto con él es la longitud de la circunferencia de la rueda.
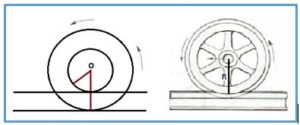
En el caso que se muestra en la figura. Si dos ruedas concéntricas soldadas, ruedan a diferentes niveles, cuando los puntos más bajos de ambas circunferencias vuelven a alcanzar el punto más bajo habrán recorrido la longitud (aparentemente), por lo tanto, ambas tendrán la misma longitud.
Lo que realmente ocurre es que el punto más bajo no ha llevado una trayectoria horizontal, sino que, por ejemplo, a mitad de su recorrido, habría alcanzado el punto más alto; ha recorrido cada punto una trayectoria diferente y no rectilínea describiendo una curva que se llama cicloide y se muestra en la figura:

Las paradojas no forman parte de una formación reglada en matemáticas, pero dar una explicación a estas paradojas, aclara las ideas, fomenta el espíritu crítico y despierta la curiosidad y el interés de los estudiantes por las matemáticas.
