
El álgebra es generosa; a menudo da más de lo que se le pide. (J. D’Alembert (1717-1783)
El álgebra comenzó siendo la rama de las matemáticas que resolvía ecuaciones numéricas. Con los métodos algebraicos, mediante las operaciones aritméticas, se podía calcular el valor de una incógnita que aparecía relacionada con valores numéricos en una ecuación.
El origen de la palabra álgebra procede del árabe y aparece en el título de la obra Hisab al-jabr wal-muqabala (ciencia de la reducción y de la confrontación o ciencia de las ecuaciones) de matemático árabe Al-Jwarizmi (780-850). Específicamente el término álgebra deriva de la palabra al-jabr, que significa restauración o reducción. Autores como M. de Cervantes (1547-1616) o F. de Quevedo (1580-1645) utilizaron en sus obras el término algebrista con el significado de cirujano reparador o componedor de huesos. Manteniendo el significado profundo de que, del mismo modo que un cirujano reducía fracturas y concertaba los huesos, el algebrista matemático establecía los procedimientos para reducir y ordenar los términos de la ecuación hasta que la incógnita quedaba despejada.
Dejando aparte los cambios que experimentó desde sus antecedentes en el Algebra Geométrica del libro II de los Elementos de Euclides y en la obra de Diofanto de Alejandría (S. III), partiremos desde el momento en el que se comenzaron a utilizar en occidente el sistema de numeración decimal posicional y los algoritmos para realizas las operaciones elementales. Es decir, desde el siglo IX, momento en que se el álgebra fue incorporada a la matemática occidental a través de la obra de Al-Jwarizmi, hasta los inicios de su transformación en Algebra Abstracta con la obra de J. L. Lagrange (1736-1813), a fínales del siglo XVIII, dejando para otros apartados de este blog, la aportación genial y transcendental de E. Galois (1811-1932) a las matemáticas así como las importantes y decisivas aplicaciones de la teoría de grupos para estructurar las matemáticas, la física y para describir el comportamiento de las partículas elementales en Mecánica Cuántica.
Al-Jwarizmi (780-850) fue el más reconocido de los matemáticos musulmanes medievales. Dio a conocer a los matemáticos europeos los números indo arábigos y en su libro Hisab al-yabr wa’l muqqabala, considerado uno de los primeros libros de álgebra, expuso el método de completar cuadrados, para resolver la ecuación de segundo grado basado en conceptos geométricos.
La traducción de la obra al latin por R. de Chester en el siglo XII en la Escuela de Traductores de Toledo difundió la obra. Autores como J. Sacrobosco (1195-1256) en el libro titulado De Algorismo describe el cálculo con enteros positivos, dando algoritmos para la suma, la resta, la multiplicación, la división, las raíces cuadradas y las cúbicas.
En siglo XIII las matemáticas se acercaron a resolver problemas de la vida práctica, con esto queremos decir que con ellas no se trataba de comprender o describir la estructura del Universo, ni llegar a expresar sus leyes de comportamiento, ni tampoco que antes del siglo noveno las operaciones aritmética necesarias para el comercio no se realizaran con precisión, sino que las nuevas matemáticas ofrecían a comerciantes, astrónomos, matemáticos, curiosos y público en general un método fácil que permitía resolver con facilidad problemas cotidianos, y dejarlos escritos, con unas reglas de cálculo sencillas.
Fibonacci, con el Liber Abaci (1202) elaboró unas matemáticas que, con las cifras indo arábigas y los algoritmos aritméticos, señalaban una nueva dirección que se separaba de la rigurosa y ardua geometría euclidiana. Los algoritmos aritméticos permitían resolver con facilidad problemas cotidianos y facilitaban el acceso al conocimiento de las matemáticas a amplios sectores de la población. El objetivo primordial del libro era poner a disposición de los comerciantes una herramienta de cálculo mucho más potente que el tradicional ábaco y que, además, se podían dejar los cálculos y los desgloses por escrito y poder comprobar los libros de cuentas. El Liber contenía cincuenta y un problemas con sus soluciones, algunos de estos problemas con métodos de resolución ingeniosos y brillantes.
Con la evolución de la notación aritmética surgieron signos para las operaciones, entre números. Por otra parte, cuando se querían dar reglas generales para determinar un valor desconocido, además de símbolos, se empleaban letras y la aritmética de los números pasó a ser la que se denominó algebra (o logística) speciosa que era el arte del cálculo con símbolos, entre los cuales se incluían las incógnitas, los parámetros, los signos de las operaciones, etc. Así el Algebra pasó por tres etapas diferentes, no precisamente cosecutivas en el tiempo, el álgebra retórica, que expresaba sus reglas y algoritmos (por ejemplo de resolución de ecuaciones) el lenguaje corriente, el álgebra sincopada que las expresaba con abreviaturas las operaciones (plus, minus, cosa, census, y el algebra simbólica en la que las operaciones (+,-, x, /, √…), las relaciones (=, ≤,<, ≥, >,..), las incógnitas (x, y, z..) y los parámetros (a,b,c..) se expresaban de forma simbólica. De este modo el Algebra se convirtió en un lenguaje lógico que se adaptaba a la resolución de los problemas más variados.
Para muchos científicos, como Th. Hobbes (1588-1679) e I. Barrow (1558-1679), los métodos del Algebra no formaban parte de las matemáticas y consideraban que el álgebra era un colección de reglas útiles con las que expresar y describir los razonamientos, en suma no pasaba de ser una eficaz con la que se podían resolver hasta problemas de Geometría de Euclides, pero con alguna incoherencia como lógica y argumentaban que, al resolver las ecuaciones algebraicas aparecían soluciones extrañas como las negativas, a lo que R. Descartes (1596-1650) en su Geometría (1637) las llamaba soluciones falsas y otras soluciones complejas que venían preocupando a los matemáticos desde el Ars Magna (1545) de G. Cardano (1501-1576).
El lenguaje fue una de aportaciones que dejó el Álgebra a las matemáticas. Superando su primer objetivo, marcado por Al-Jwarizmi, que era el de resolver problemas con ecuaciones. La aplicación del lenguaje algebraico a la Geometría transformó a esta rama de las matemáticas. F. Vieta (1540-1603) asoció el problema de la trisección de ángulos a la resolución de una ecuación de tercer grado. P. Fermat (1601-1665), que conoció en Burdeos el Algebra y el simbolismo de Vieta, escribió su obra Ad locos planos et solidos isagoge (1636) (Introducción a los lugares planos y sólidos), y, aplicando el lenguaje algebraico de Vieta, demostró que las curvas que se podían expresar mediante ecuaciones de primer y segundo grado (en dos variables) eran las rectas y las cónicas. También estableció que, en general, cada curva tenía una ecuación asociada y que una ecuación algebraica representaba siempre una curva, entre los primeros ejemplos que aportó están las parábolas de Fermat: y = xn, si n >0 (o hipérbolas si n <0). Fermat también empleó el cálculo literal para problemas de optimización y trazado de tangentes abriendo el camino al cálculo infinitesimal. R. Descartes proporcionó métodos con los cuales los problemas de la geometría plana se podían expresar en lenguaje algebraico y resolverlos. Con esta consecución el lenguaje algebraico, no sólo ganaba terreno en el campo de las matemáticas, sino que se consolidaba como algo coherente capaz de expresar con él toda la Geometría con lo que daba indicios de tener una coherencia semejante a la de la Geometría.
Cuando se aplicaban las fórmulas de resolución de ecuaciones aparecían nuevos tipos de números aunque se plantearan problemas cotidianos en los que se esperaban soluciones reales positivas. A las operaciones con estos nuevos números se les presuponía que disfrutaban de propiedades análogas y compatibles con las de los números reales. Rafael Bombelli (1526-1672) encontró, resolviendo la ecuación x3 = 15 x+4, de la que sabía que poseía la solución x = 4, que usando fórmula de G. Cardano para la cúbica se obtenía una solución, en la que aparecía la siguiente expresión:
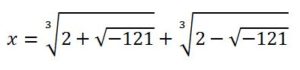
Y aunque sabía que las raíces cuadradas de números negativos no podían existir en el campo de los números reales, ya que ningún número real elevado al cuadrado puede dar un número negativo, aplicando las reglas adecuadas de suma y multiplicación, encontró soluciones que hasta entonces no se entendían. Y que esa expresión tan complicada tenía un valor x = 4.
En este sentido decía J. D’Alembert que el álgebra era generosa; y que a menudo daba más de lo que se le pedía, en el sentido de que siempre respondía más de lo que se le preguntaba. Precisamente fue D’Alembert enunció en 1742 e intentó demostrar por primera vez el Teorema Fundamental del Álgebra: toda ecuación algebraica con coeficientes reales de grado n con tiene n soluciones complejas. En ese momento se creía que las ecuaciones algebraicas de cualquier grado se podrían resolver mediante expresiones radicales.
Con lo anterior podemos decir que el álgebra permitió el descubrimiento de nuevos número cuando sólo se buscaban soluciones positivas.
El Álgebra se convirtió en el lenguaje de la Geometría y se convirtió en el lenguaje en el que se expresó el Cálculo Infinitesimal y permitió descubrir nuevos conjuntos numéricos. Pero aún podemos destacar otras portaciones importantes del Álgebra. Y son los cambios fundamentales que se produjeron en ella en el siglo XIX en un proceso que comenzó con Lagrange en el último cuarto del siglo XVIII y fue el primer paso del Álgebra Clásica al Algebra Abstracta o Álgebra de Estructuras.
En los comienzos del Algebra, que llamaremos Álgebra Clásica, sus elementos eran los números y las letras para representar incógnitas y parámetros y las operaciones eran las aritméticas. En los libros de Álgebra Abstracta encontramos más símbolos que letras porque los elementos con los que trabaja no son sólo números. En ésta Álgebra los vectores ya no se consideran como ternas de números reales, son elementos que se tratan con independencia de todo sistema de referencia y sus elementos sino elementos de un cuerpo arbitrario. La generalización se produce cuando se cummplen los mismos teoremas cuando los escalares no son números reales, sino elementos de cualquier cuerpo algebraico. Muchas ramas de Álgebra Clásica se reformularon y se aclararon bajo las abstracción de la nueva Álgebra de estructuras. La Teoría de Galois que se formuló inicialmente como el estudio de las sustituciones de las raíces de un polinomio se reformuló como el grupo de automorfismos del cuerpo engendrado por ellas. Aparece el álgebra de matrices como el álgebra de las aplicaciones lineales y ya se retira el foco de los números y sus operaciones y de estudian las relaciones entren ellos con ayuda de otros conceptos y otros símbolos que ayudan a pensar y a manejar los conocimientos algebraicos de forma más general y sencilla.
Esta evolución, que parece una ruptura, es el resultado de los infructuosos intentos realizados durante casi tres siglos por los matemáticos para encontrar una fórmula para resolver mediante radicales la ecuación algebraica de quinto grado.
Desde mediados del siglo XVI los algebristas disponían de fórmulas para resolver las ecuaciones algebraicas por radicales para las ecuaciones algebraicas hasta cuarto grado. Las fórmulas fueron publicadas por Cardano en su Ars Magna (1545) y, desde entonces se buscaba obtener una expresión semejante para ecuaciones de grado superior a cuatro.
El avance definitivo en la dirección correcta, que sirvió para resolver el problema y orientar el Algebra Clásica hacia el Algebra Abstracta lo dio J.L. Lagrange, el cual realizó una revisión de los métodos utilizados hasta entonces en la resolución de ecuaciones algebraicas de tercer y cuarto grado y publicó sus resultados en Reflexiones sobre sobre a resolución algebraica de ecuaciones (1770).
Lagrange recuperó una serie de ideas como dada a conocer por J. Hudde (1628-1704) que decía que Todo número complejo tenía tres raíces cúbicas. Si z es una raíz cúbica de un número complejo Z, como la unidad tiene tres raíces cúbicas que son:
1, 𝜔 = – 1/2 + (1/2) √-3 𝜔2 = – 1/2 – (1/2) √-3
Entonces la tres raíces cúbicas de Z son:
z, 𝜔z, 𝜔2z
Lagrange observó que, cuando se resolvía la cúbica x3 + px – r = 0, haciendo el cambio de variable x = u + v y estableciendo la relación v = –q/3u se obtenía una ecuación resolvente:
u6 – ru – q3/27 = 0
que era una ecuación cuadrática en u3, que se sabía resolver.
En esta descripción no se necesita comprender la solución completa de la ecuación cúbica, sólo nos interesa saber que las raíces de una ecuación cúbica se pueden escribir en función de las raíces de otra ecuación que si sabemos resolver que se llama resolvente. Lagrange observó que las raíces de la ecuación resolvente de la cúbica se podían expresar en función de las raíces originales α1, α2, α3 de una forma simétrica:
| v =(1/3)( α1+𝜔 α2 + 𝜔2 α3) |
u =(1/3)( α1+𝜔 α3 + 𝜔2 α2) |
| 𝜔v =(1/3)( α3+𝜔 α1 + 𝜔2 α2) | 𝜔u =(1/3)( α2+𝜔 α1 + 𝜔2 α3) |
| 𝜔2v =(1/3)( α2+𝜔 α3 + 𝜔2 α1) | 𝜔2u =(1/3)( α3+𝜔 α2 + 𝜔2 α1) |
Y que todas las expresiones se podían obtener a partir de una de ellas permutando α1, α2, α3 de las seis formas (3!) posibles. Ahí estaban escondidos los grupos de sustituciones y los comienzos del álgebra abstracta. Entonces, apoyándose en el teorema fundamental podía construir la resolvente de la ecuación, que en el caso de la cúbica sería el producto de seis factores de primer grado que llamando uijk=(1/3)( αi+𝜔 αj + 𝜔2 αk) sería:
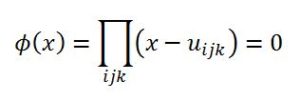
Y mediante las uijk se podían expresar las raíces de la cúbica. Lo mismo sucedía para la ecuación de cuarto grado, pero no se consiguió hallar una ecuación resolvente para la ecuación de quinto grado.
Debemos recordar que a partir de que D’Alembert formulara el Teorema Fundamental del Álgebra se sabía que la ecuación algebraica de quinto grado tenía cinco soluciones complejas, con lo que el problema de resolver la ecuación de quinto grado no era un problema de existencia de soluciones, sino de saber si sus raíces podían expresarse o no en función de los coeficientes de la misma con fórmulas semejantes a las de Cardano.
P. Ruffini (1765-1822) presentó en Teoría general de las ecuaciones (1799) una demostración de la irresolubilidad de la ecuación de quinto grado mediante radicales. Ruffini demostró que no existía una ecuación resolvente para las ecuaciones mayores o iguales a cinco. En 1823 N. Abel demostró de forma completa del mismo teorema y, finalmente Galois demostró que soluciones de una ecuación polinómica se pueden expresar en la forma de Cardano si y sólo si el grupo de Galois de dicha ecuación era resoluble. Este tema, más específico, lo trataremos más adelante.




