“Investigué sobre la influencia de la escala en la resistencia de materiales y estructuras. Por ejemplo, comprobé que los huesos de un animal grande deben ser proporcionalmente mucho más grandes que los huesos semejantes de un animal pequeño. Y descubrí que eso sucede porque el peso crece más deprisa que la resistencia de los huesos: un animal dos veces mayor que otro tiene cada hueso dos veces mayor y cuatro veces más resistente, pero el animal será ocho veces más pesado…” Galileo Galilei
La ley cuadrado cúbica fue descubierta y enunciada en 1638 por Galileo Galilei (1564-1642) en su obra Discursos y demostraciones matemáticas en torno a dos nuevas ciencias referidas a la mecánica y a los movimientos locales. En la obra pone límites al aumento de tamaño de los objetos y de los seres vivos manteniendo la misma forma. Por ejemplo, la ley establece y justifica porqué en el mundo real no se pueden existir hormigas del tamaño de una persona manteniendo su forma de hormiga. La ley cuadrado cúbica de muestra que la hormiga de tamaño humano y hecha a escala de la hormiga normal se movería lentamente con una estructura corporal que no soportaría su peso o caería aplastada por su propio peso. La ley dice que:
Cuando un objeto crece manteniendo su forma y sus proporciones, su superficie aumenta con el cuadrado de una longitud característica del mismo (por ejemplo la altura) y en cambio su volumen aumenta con el cubo de esa misma longitud.
En resumen, que el volumen (que se corresponde con el peso) aumenta en mucha mayor proporción que la superficie. Un ejemplo fácil que se suele emplear para explicar esta afirmación es un cubo. Un cubo de 10cm de lado tiene un volumen 1000cm3 y la superficie de una de sus caras es de 100cm2. Si se duplica su lado, su volumen será ahora de 8000cm3 y su superficie de 400cm2. Es decir su volumen ha aumentado 8 veces (2 al cubo) y sin embargo, su superficie sólo 4 veces (2 al cuadrado)
Esta propiedad podemos extenderla a los animales y al ser humano, de forma que si duplicamos la altura de una persona (por ejemplo si pasa de 1,80m a 3,60 m) y aumentamos en la misma proporción las demás medidas, cualquier volumen de nuestra anatomía (cabeza, piernas o brazos se habrá multiplicado por 8 (2 al cubo) y cualquier superficie nuestra de nuestro cuerpo (la palma de la mano, la sección de lo huesos, la planta de los pies e incluso la superficie total de nuestra piel) se habrá multiplicado por 4 (2 al cuadrado)
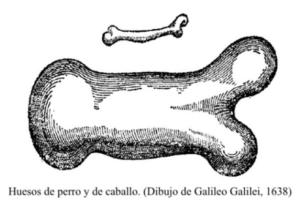
Lógicamente, todas las propiedades humanas que dependan del volumen (como, por ejemplo, el peso o capacidad estomacal) aumentarán en la misma proporción que el volumen. Mientras que las propiedades que dependan de la superficie (como la resistencia de los huesos o la ventilación pulmonar) aumentarán en la misma medida que la superficie.
Del mismo modo, el peso de una viga aumenta con el cubo de su longitud , mientras que su resistencia crece con la sección que aumenta con el cuadrado. La ley cuadrado-cúbica es una lucha entre los exponentes dos y tres.
Jonathan Swift (1667-1745) en su libro Viajes de Gulliver (1726), describe las aventuras fantásticas de Gulliver, en el país de Liliput. En este país todos los seres vivos eran semejantes a los que existían en nuestro mundo, pero de un tamaño doce veces menor y cuenta como el rey de Liliput le asignó la cantidad de comida diaria con la ley cuadrado cúbica:
«El emperador dispuso que me fuera suministrada una cantidad de comida y bebida bastante para el mantenimiento de 1.728 liliputienses. Pregunté algún tiempo después a algún amigo mío de la corte cómo se le ocurrió fijar ese número precisamente, y me contestó que los matemáticos de Su Majestad, habiendo tomado la altura de mi cuerpo por medio de un cuadrante y visto que excedía a las suyas en la proporción de 12 a 1, dedujeron tal cantidad».
Los matemáticos del rey habían determinado la ración diaria de comida de Gulliver con el siguiente razonamiento: si un liliputiense tomaba un determinado volumen de comida al día, Gulliver, como Gulliver era doce veces más alto que un liliputiense, debería tomar un volumen de comida de 123 = 1728 unidades.
Gulliver también describe sus aventuras en Brobdingnag, el país de los gigantes que eran doce vece más altos que Gulliver, y los que se puede decir lo siguiente: Por ser el peso de un gigante 1728 veces mayor que el peso de Gulliver y las plantas de los pies del gigante 144 veces mayor que las plantas de los pies de Gulliver. La presión aplicada sobre el suelo a caminar un gigante sería doce veces mayor que la de Gulliver y el pavimento se hundiría como se hunde la superficie de las calles peatonales al paso de algunos camiones de reparto.
La ley cuadrado cúbica también permite explicar por qué las montañas no superan cierta altura; una montaña de veinte de kilómetros de altura se derrumbaría por su propio peso.
