En este escrito voy a olvidarme del algoritmo que tradicionalmente se ha enseñado en las Aritméticas del siglo pasado y que hoy día, en la práctica, ha quedado relegado desde la aparición de las calculadoras y de los ordenadores. En la actualidad pocos profesionales realizan las operaciones aritméticas con lápiz y papel, por esta razón voy a exponer unos métodos alternativos para calcular la raíz cuadrada que nos hacen profundizar en los algoritmos y adoptar diferentes puntos de vista a la hora de realizar un cálculo.
1.- MÉTODO ITERATIVO DE PUNTO FIJO
El método iterativo de punto fijo se suele emplear para hallar soluciones de una ecuación f(x) = 0, si puede expresarse en la forma: x = g(x). Entonces, partiendo de un valor inicial x0 , se puede calcular la sucesión de valores
x0 , x1 = f(x0 ), x2 = f(x1 ), x3 = f(x2 ), …, xn = f(xn-1 ), …
que, si es convergente, su límite, a, será el punto fijo de la función x = g(x), y será una solución de la ecuación f(x) = 0. Por lo tanto, hallar las raíces de la ecuación f(x) = 0, equivale a hallar los puntos fijos de g(x)
El punto fijo tiene unas propiedades importantes que se pueden resumir en este
Teorema: Si g: [a, b] ⤍ R y g(x) ∈ [a, b] para todo x ∈ [a, b], entonces g(x) tiene un punto fijo en [a, b]. Además, si g(x) no cumple más condiciones, ese punto fijo no tiene por qué ser único. Pero, si existe la derivada g’(x) existe en (a, b) y |g’(x)| <1 para todo x ∈ (a, b), entonces g(x) tiene un único punto fijo en [a, b].
Veamos dos métodos iterativos para calcular la raíz cuadrada
1.1.- METODO DE HERON PARA CALCULAR √N.
Partimos de un valor aproximado de √N, x0, y calculamos N/x0, así calculamos los lados de un rectángulo de área N. Pero, en realidad, estamos buscando el lado de un cuadrado de área N, Para aproximarnos más al lado del cuadrado, que es √N, tomamos la media de los lados obtenidos y definimos como función de iteración g(x):
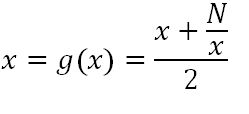Calculamos:
Que lo tomamos como nueva aproximación de la raíz cuadrada y obtenemos un nuevo valor x2, y, con él x3 y así sucesivamente obtenemos la sucesión:
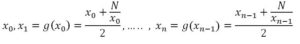
Ejemplo: Calcular √13 con cinco iteraciones, partiendo de x0 = 2,5
Con la Hoja de Cálculo Excel obtenemos:
x0 = 2,5 x1 =3,85 x2 = 3,61331169 x3 = 3,60555961
x4 = 3,60555128 x5 = 3,60555128
1.2.- MÉTODO DE ERRORES PARA CALCULAR √N.
Partimos del valor aproximado x0 y suponemos que cometemos un error a, entonces se cumple:
(x0+ a)2 = N ⇒ x02 + 2a x0 + a2 = N
Desestimando a2 resulta que : x02 + 2a x0 = N de dónde:
Para aproximarnos más al lado del cuadrado, que es √N, tomamos como función de iteración g(x):
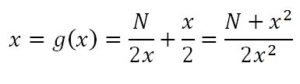
Y partiendo de x0 obtenemos la sucesión:
Ejemplo: Calcular √23 con seis iteraciones, partiendo de x0 = 2,5
Con la Hoja de Cálculo Excel obtenemos:
x0 = 2,5 x1 = 5,85 x3 = 4,89081197 x4 = 4,79675379
x5 = 4,79583161 x6 = 4,79583152 x7 = 4,79583152
ESTE MÉTODO SE PUEDE EXTENDER AL CÁLCULO DE RAÍCES CÚBICAS
Partimos del valor aproximado x0 y suponemos que cometemos un error a, entonces se cumple:
(x0+ a)3 = N ⇒ x03 + 3a2x0 + 3ax02 + a3 =N
Desestimando a2 y a3 resulta que : x03 + 3ax02 = N de dónde:
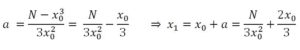
2.- EL MÉTODO ARITMÉTICO PARA CALCULAR LA RAIZ ENTERA DE √N
Este método se basa en que la suma de los n primeros números impares es n2, es decir:
1 + 2 + 3 + … + (2n-1) = n2
Cualquier número entero positivo N o bien es cuadrado o se encuentra entre dos cuadrados consecutivos:
1 + 2 + 3 + … + (2n-1) = n2 ≤ N ≤ 1 + 2 + 3 + … + (2n+1) = (n+1)2
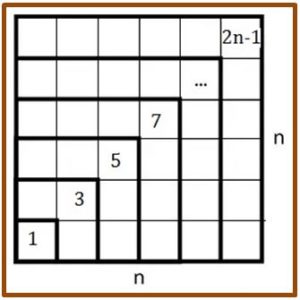
El método consiste en restar a N sucesivamente números impares hasta que al restarme en siguiente de un número negativo. La raíz entera por defecto será el número de impares que le hayamos restado y lo que queda es el resto de la raíz
Ejemplo: Para calcular la raíz de 45
A 45 le podemos restar 1, 3, 5, 7, 9, 11 y que suman 36, pero con siguiente impar, 13, sumaría 49 que haría que 45-49 sería negativa
45 – 1 – 3 – 5 – 7 – 9 – 11 = 45 – (1 + 3 + 5 + 7 + 9 +11) = 45 – 36 = 9
La raíz entera será el número de impares dentro del paréntesis y el resto de la raíz cuadrada 9
Ejemplo: √135
135 – (1+3+5+7+9+11+13+15+17+19+21) =135 -121 = 14,
la raíz entera es 11 ( Se le han restado 11 impares) y el resto 14.