El principio del palomar fue enunciado por Dirichlet en 1834 y dice lo siguiente: Si n palomas ocupan m nidos y n > m, entonces en un nido habrá al menos dos palomas.
Otra formulación, que proporciona algo más de información, es la siguiente:
Si distribuimos am + n palomas en m nidos, y n ≥ 1, entonces habrá algún nido que contenga al menos a + 1 palomas.
A continuación presentamos unos problemas de enunciado geométrico que pueden resolverse utilizando el Principio del Palomar.
Problema 1.– Demostrar que entre cinco puntos cualesquiera dentro de un triángulo equilátero de lado dos hay al menos dos de ellos están a una distancia menor o igual que 1.
Solución: Sabemos que si en un triángulo equilátero cualquiera seleccionamos dos puntos P y Q, la máxima distancia que los puede separar es la longitud de su lado.
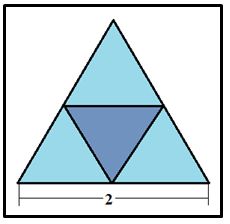
Si dividimos el triángulo equilátero de lado dos en cuatro triángulos equiláteros iguales como se muestra en la figura, entonces podemos suponer que los cinco puntos elegidos al azar serán las palomas y los cuatro triángulos de lado uno los nidos. Entonces, por el principio del palomar, necesariamente habrá dos puntos en alguno de los triángulos pequeños. Como la máxima distancia entre dos puntos de un triángulo equilátero de lado uno es uno y hay dos puntos en uno ellos a una distancia menor o igual que uno.
Problema 2.– Señalamos diez puntos al azar en un cuadrado de lado unidad. Demostrar que hay al menos dos de ellos que están a una distancia menor o igual que √2/3.
Solución: Sabemos que si en un cuadrado seleccionamos dos puntos P y Q, la máxima distancia que los puede separar es la longitud de su diagonal.

Para resolver el ejercicio por el principio del palomar supondremos que los puntos son las palomas y los palomares los son los nueve en cuadrados iguales en los que se divide el cuadrado inicial de lado unidad como se ve en la figura:
Como tenemos 10 puntos a distribuir entre 9 cuadrados, al menos existirá uno de los cuadrados de lado 1/3 que contenga dos puntos y la distancia entre ellos será menor que la diagonal que es √2/3.
Problema 3.– Se toman 28 puntos al azar en el interior de un cubo de lado 3. Prueba que hay al menos dos puntos que están a una distancia menor o igual que √3
Solución: De modo análogo al problema anterior los 28 puntos serán las palomas y si dividimos el cubo en 27 cubos de lado unidad que serán los nidos. Luego en alguno de los cubos de lado unidad debe haber dos puntos y la distancia entre ellos debe ser menor que √3.
Problema 4.- En un hexágono regular de tres metros de lado pintamos al azar 365 puntos rojos distintos. Demostrar que hay al menos siete de ellos están a una distancia menor o igual a un metro
Solución: Los puntos serán las palomas. Dividimos el hexágono regular en triángulos equiláteros de lado un metro de siguiente modo:
Trazando sus diagonales mayores, el hexágono queda dividido en seis triángulos equiláteros de lado 3 m. Cada uno de estos triángulos puede dividirse, a su vez, en nueve triángulos equiláteros de lado 1 metro y cada uno de esos cincuenta y cuatro triángulos equiláteros de lado unidad será un nido
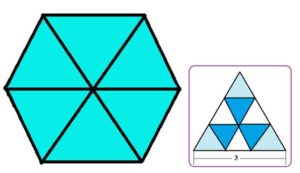
De esta forma tenemos 365 puntos (palomas) y los 54 triángulos equiláteros de lado unidad (nidos), Como 365 = 54 × 6 + 41 entonces, aplicando el Principio del Palomar hay al menos uno de los triángulos de lado unidad que contiene al menos 7 puntos rojos, que estarán a una una distancia igual o menor que un metro.
Problema 5. Demostrar que entre cinco puntos del plano con coordenadas enteras hay dos cuyo punto medio también tiene coordenadas enteras.
Solución: (el punto medio de los puntos, A = (a, b) y B = (c, d) del plano es:
![]()
Observemos que la única forma de que las coordenadas de M sean enteros es que las abscisas y las ordenadas de ambos puntos tengan la miasma paridad. Es decir que a tenga la misma paridad que c y b la misma paridad que d.
Cada punto puede tener las coordenadas de una de siguientes cuatro formas:
(Par, Par), (Par, Impar), (Impar, Par), (Impar, impar).
Aplicando el Principo del Palomar estas estas cuatro formas serán nuestros nidos y los cinco puntos del plano serán las palomas. Por lo tanto, habrá dos puntos de una de las cuatro formas y el punto medio de ambos tendrá coordenadas enteras.
Problema propuesto. Demostrar que dados nueve puntos en el espacio tridimensional con coordenadas enteras siempre hay un punto de coordenadas enteras entre algún par de ellos.
Indicación: Razonamiento semejante al anterior en el espacio las paridades de las coordenadas de cada punto se dan de ocho forma diferentes como:
(P,P,P), (P,P,I), (P,I,P), (P,I,I), (I,P,P), (I,P,I), (I,I,P), (I,I,I)