PROBLEMAS CON TRIÁNGULOS RECTÁNGULOS Y SUS SEMEJANZAS

PROBLEMA 1: Sobre la hipotenusa de un triángulo rectángulo ABC de medidas AB =12 cm,  AC = 9 cm y BD = 15 cm. Se señalan los puntos M y N, de manera que CM = 3 cm,    MN = 5 cm  y NB = 7 cm. Calcular las áreas de los triángulos ACM, AMN y ANB.

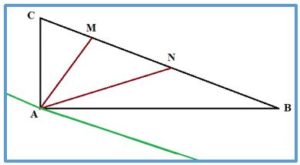
Solución 1: El área del triángulo ABC es = 12 ·9 /2 = 54 cm².

Los triángulos ACM, AMN y ANB, tomando como base la línea de la hipotenusa tienen la misma altura (la distancia de la hipotenusa a la paralela a ella trazada por el vértice A). Por lo tanto, el área será directamente proporcional a la medida de la base. Las áreas se calculan haciendo un reparto proporcional a 3, 5,y 7 del área del triángulo ABC , es decir:

Área de ACM = 54·3/15 = 10,8 cm² ,

Área de AMN = 54·5/15 = 18 cm² y

Área de ANB= 54·7/15 = 25,2 cm²

Otra forma de abordar el problema es observar que la altura de los res triángulos ACM, AMN y ANB es precisamente la altura relativa a la hipotenusa, h,  del triángulo ABC, que tiene 54 cm² de área. Por tanto, se cumplirá:

54 = 15·h/2   ⇒  h = 7,2 cm

Área de ACM = 3·7,2/2 = 10,8 cm² ,

Área de AMN = 5·7,2/2 = 18 cm² y

Área de ANB= 7·7,2/2 = 25,2 cm²

PROBLEMA 2.- Área del triángulo rectángulo verde sabiendo que ABC es un triángulo rectángulo en A , MN paralela a AB , NP paralela a AC las medidas que se indican.

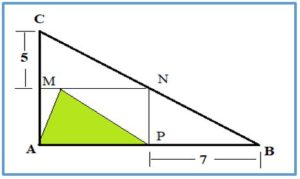
Solución: El área del triángulo verde es a mitad del área del rectángulo MAPN. Si hacemos AP = x   y AM = y, como ABC, MNC y PBN  son triángulos semejantes, se cumple que:

De donde:

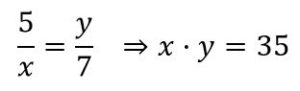
Como x·y = 35 es el área del rectángulo, entonces el área de triángulo verde será 35/2 = 17,5

PROBLEMA 3.- Área del triángulo verde sabiendo que ABC es un triángulo rectángulo en A , AC = 9   AB  = 12    y  CD =15,  CM = AC  = 9

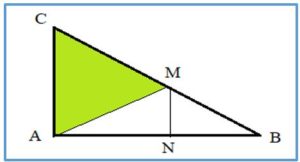
1. ¿Cuánto mide la altura MN del triángulo AMB?
2. Área del triángulo isósceles ACM
3. Perímetro del triángulo isósceles
4. Altura del triángulo isósceles

Solución:

1.- La altura de AMB, MN, es paralela al lado AC, por tanto:  El triángulo ABC es semejante al MNB y se verifica:

AC/MN = CB/MB    ⇒ 9/MN = 15 /6

⇒ MN =54/15 = 18/5 = 3,6 cm

2.- Area de ACM = Área de ACB – Area de AMB = AB·AC /2 – AB· AM /2 =

= 12·9/2 – 12·3,6/2 =  54 – 21,6= 32,4 cm²

3.- Perímetro del triángulo isósceles: Calcularemos AM: AM² = AN² + MN²para calcular AN: 9/AN = 6/12-AN   ⇒ 108-9AN = 6AN   ⇒  108 = 15 AN   ⇒  AN = 7,2.   AM² = AN² + MN²     ⇒   AM² = 7,2² +3,6² = 64,8  ⇒  AM = 8,05 cm, luego  el perímetro será 9 + 9 + 8,05 = 26,05 cm

4.- Altura del triángulo isósceles: Como  Area ACM =  AM·h/2   ⇒  32,4 = 8,05·h /2  ⇒  h = 8,05 cm