PROBLEMA 1.- Trece pollitos estaban picoteando granos de trigo. El primero comió 60 granos, el segundo, 40, y cada pollito siguiente comió la media aritmética de los anteriores. ¿Cuántos granos comió el ultimo?
Solución:
Observemos que si el primero come a, el segundo come b el tercero comerla la media
El tercero comerá (a+b)/2, el cuarto comerá la media de los tres primeros:
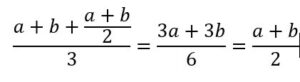
El cuarto quinto, el sexto… comerán el mismo número de granos que la media de los dos primeros
(Si la media de unos números a, b, c, d … es m, la a media de a, b, c, d … m es m, es decir, la nueva media no cambia). El pollito nº 13 se habrá comido 50 granos, que es a media de los dos anteriores.
PROBLEMA 2.- Descompón el número 168 en tres sumandos enteros que estén en progresión geométrica tales que la diferencia entre el mayor y el menor sea 120:
Solución: Las condiciones se expresan en el siguiente sistema (1), (2):
a + ar + ar2 = 168 (1) ar2 – a = 120 (2) ⇒ (restando las ecuaciones)
⇒ ar + 2a = 48 a(r + 2) = 48 ⇒ a = 48/(r+2) ⇒ (Sustituyendo en (2) y operando)⇒
⇒ 120 (r+2) = 48r2 – 48 ⇔ 5 (r+2) = 4r2 – 4 ⇒ (resolviendo la ecuación) r = 4 y a= 8
Los tres sumandos serán 8, 32 y 128
PROBLEMA 3.-. ¿Es posible encontrar diez números naturales consecutivos de manera que la suma de sus cuadrados sea igual a la suma de los cuadrados de los nueve números naturales consecutivos que les siguen?
Solución. Denotemos los diez números consecutivos como (n – 9), …,(n – 1), n. Según la condición
(n – 9)2 + … + (n – 1)2 + n2 = (n + 1)2 + … + (n + 9)2
operando, obtenemos que:
10 n2 – 90n = 9n2 + 90n ⇒ n2 = 180n, De aquí, n = 180,
Los diez números son 171, 172, 173, 174 175, 176, 177, 178, 179, 180
PROBLEMA 4. Se considera un numero n de cuatro cifras, cuadrado perfecto, tales que todas sus cifras son menores que 6. Si a cada cifra se le suma 1, el número resultante es otro cuadrado perfecto. Hallar n .
Solución:
Sea n2 el número buscado, aumentar cada una de sus cifras en una unidad es sumarle 1111 y el número obtenido será cuadrado perfecto, m2.
Los números m2– n2 = 1111 ⇒ m2– n2 = 11·101 , ⇒ (m+m) (m-n) = 11·101
Como 11 y 101 son primos entre si
m + n = 101 y m – n = 11 ⇒ 2m = 112, m = 56 y n = 45
Por tanto, los números son:
⇒ n2 = 2025 y m2 = 3136
El sistema m + n = 11 y m – n = 101 ⇒ 2m = 112, m = 56 , n = – 45
PROBLEMA 5 . Se tiene una progresión aritmética en la cual la suma de un numero cualquiera de términos es siempre el triple del cuadrado del número de términos. Determina la progresión. Hallar el termino de lugar 2025.
Solución: Sea los n términos de la progresión aritmética cuyo primer término es a y la diferencia d: a, (a+d), (a+2d), …. , (a+(n-1)d)
La suma a + (a+d)+ (a+2d)+ …. + (a+(n-1)d) = 3n2 ⇒ na + dn(n-1)/2 = 3n2 ⇒
⇒ 2na + dn(n-1) = 6n2 ⇒ 2a + d(n-1) = 6n (1)
Si n =1 ⇒ 2a = 6 ⇒ a =3
Sustituyendo el valor de a = 3 en (1):
6 + d(n-1) = 6n ⇒ d(n-1) = 6n – 6 ⇒ d(n-1) = 6(n – 1) ⇒ d = 6
La progresión será: 3, 9, 15, 21, 27,…, 3+6(n-1)
El término a2025 = 3 + 2024·6 = 12.147