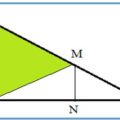
En este apartado vamos hacer algunos ejercicios sobre los triángulos semejantes que aparecen al trazar la altura relativa a la hipotenusa de un triángulo rectángulo. El Teorema de la altura dice:
La altura relativa a la hipotenusa es media proporcional entre los segmentos que determina sobre ella.
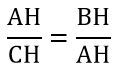
La demostración se basa en que los triángulos: AHC, AHB y ABC son semejantes por tener los ángulos correspondientes iguales
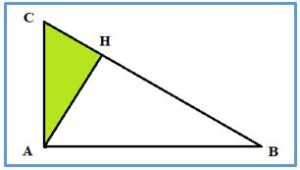
Problema 1.- Área del triángulo rectángulo verde sabiendo que ABC es un triángulo rectángulo en A , AC = 9 m AB = 12m y CB =15 m y AH es la atura relativa a la hipotenusa del triángulo.
Solución:
Los triángulos ABC y HCA son semejantes
Razón de semejanza (cociente de hipotenusas) = AC/CB = 9/15 = 3/5
Razón entre las áreas = (Cuadrado de razón de semejanza) = (3/5)2= 9/25
Área de ABC = AB·AC/2 = 9·12/ 2 = 54m2
Área de HCA = 54·(9/25) = 486/25 = 19,44 m2
Solución trigonométrica 1:
CH = CA·sen B = 9·sen B = 9·(9/15) = 5,4 m y
AH = CA·cos B = 9·(12/15) = 36/5 =7,2 m
Área AHC = (5,4·7,2)/2 = 19,44 m2
Solución trigonométrica 2:
Área AHC = (HC·HA)/2 = 9·sen(CAH)·9·cos (CAH)/2 =
= 9·(AC/CB)·9·cos (AB/CB)/2 =
= 9·(9/15).9·(12/15)/2 = (27/5)·(36/5)/2 =19,44 m2
Problema 2.- Dado el triángulo rectángulo ABC. Calcula el área triángulo IV en función de los lados del triángulo ABC.
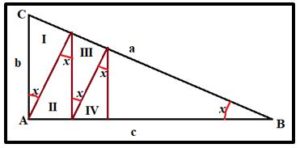
Solución: Expresaremos las medidas de los lados de los triángulos en el orden: Hipotenusa, cateto mayor, cateto menor.
Triángulo I: (b, b·cos x, b·sen x)
Triángulo II: (b·cos x, b·cos2 x b·cos x·sen x)
Triángulo III: ( b·cos2 x, b·cos3 x, b·cos2 x·sen x)
Triángulo IV: ( b·cos3 x, b·cos4 x, b·cos3 x·sen x)
Teniendo en cuenta que el área es la mitad del producto de los catetos:
Area IV = ( b·cos4 x, b·cos3 x·sen x)/2 = (b2 cos 7x·sen x)/2 =
= (b2·(c/a)7·(b/a)) /2 = (b3·c7)/2a8
Como la razón de semejanza entre un triángulo y el siguiente es cos x, la razón entre las áreas es cos2 x, por tanto
Area IV = (Area I)· cos 6x = (b·cos x·b·sen x ·cos 6x) =
= b2 cos7x· senx = (b2(c/a)7x· (b/a))/2 =(b3·c7)/2a8