Problema 1.- En un cuadrado de lado 1 cm, con los datos que se indican en la figura, calcular el área de la parte coloreada. (punta de flecha).
Solución:
Esa es una forma de dividir un cuadrado en dos partes en figuras con las que se puede rellenar el plano. Estas dos figuras han sido estudiadas en la teoría de los mosaicos y se denominan cometa y punta de flecha. La teoría de mosaicos o teselaciones estudia las diferentes maneras en las que una superficie puede cubrirse mediante larepetición de un número reducido de objetos originales, sin hacer superposiciones ni dejar huecos.
Observando la figura observamos en primer lugar que ADO y ODC son triángulos isósceles (sus ángulos miden 45º, 67º 30’ y 67º 30’) Por tanto, AD = DO =1 cm
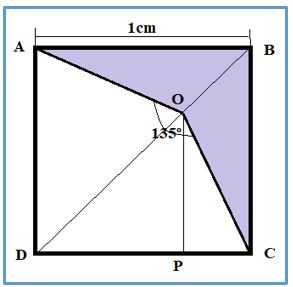
El triángulo OPD es rectángulo e isósceles (los catetos OP = PD la hipotenusa es DO = 1 cm), por lo tanto:
Área ODC = (1·1/√2)/2 = 1/(2√2) cm2 = √2/4 cm2 = Área ODA , por tanto:
Área de la cometa AOCD = Área ODC+ Área ODA = 2 Área ODC
Área de la cometa AOCD = 2(√2/4) = √ 2/2 cm2.
Área de punta de flecha ABCO = 1 – √2/2 = (2-√2)/2 cm2.
Problema 2.- Dentro del rectángulo ABCD de lados 8 cm y 5 cm se construye el cuadrado A’B’C’D’ de lado 4cm ¿Qué área tiene el triángulo sombreado?
Solución:
El teorema de la paralela media:
BC = 2·QB’ ⇒ BC = 5 cm y QB’ = 5/2 cm, por lo tanto:
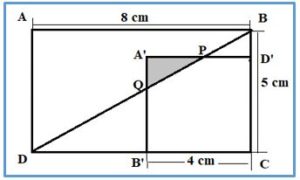
QA’ = 3/2 cm
Los triángulos rectángulos BCD y QA’P son semejantes y podemos calcular A’P
QA’/BC = A’P/DC ⇒ 1,5/5 = x/8 ⇒ x = A’P = 12/5 cm
Área QA’P = (QA’·A’P)/2 = (3/2·12/5)/2 = 36/20 = 9/5 cm2.
Problema 3.- La figura sombreada se ha obtenido de octógono regular de 2 cm de lado En un octógono regular de lado 2 cm al que se le han quitado los dos cuadrados BCQP y GFSR de construidos sobre lados BC y GF del octógono. ¿Cuál es su área?
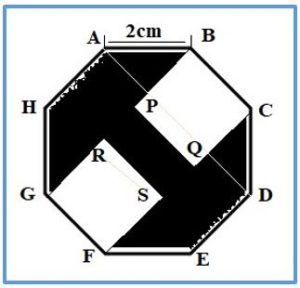
Solución: Consideremos el triángulo rectángulo isósceles APB, cuya hipotenusa mide 2 cm.
Fácilmente se calcula AP = PB = √2 cm.
El trapecio ABGH tiene de base menor 2 cm, base mayor 2 + 2√2 cm y altura √2 cm:
El área de ABGH = 3 + √2 cm2
Área de PQSR = Área de BCFG – Área BCQP – Área RSFG =
= 2·(2 + 2√2) – 4 – 4 = 4√2 – 4 cm2
Area = 2·(3 + √2) + 4√2 – 4 ) = 2 + 6√2 cm2
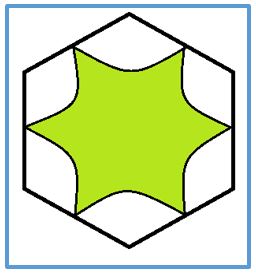
Problema 4.- Con centro en cada uno de los vértices de un hexágono de lado 6 cm trazado un arco de circunferencia de radio 3cm, como se observa en la figura. Calcular el área de la figura coloreada.
Solución:
El radio de la circunferencia es igual a lado del hexágono inscrito en la misma. Cada un arco de circunferencia determina un sector de 120º y radio 3 cm y todos juntos forman dos círculos de radio 3.
Área del hexágono = Perímetro·apotema/2 = 36·(6√3/4) = 54√3 cm2.
Área del círculo = 9π cm2.
Área de la figura coloreada= 54√3 – 2·9π = 54√3 – 18π cm2
Problema 5.- Calcula el área del octógono sabiendo que el área del trapecio coloreado es de 3 cm2.
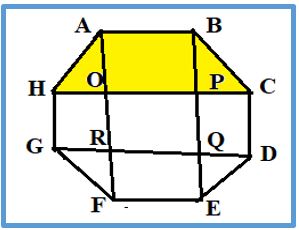
Solución 1: Llamaremos a al lado del octógono, Por tanto el trapecio ABCH tendrá las siguientes medidas: a, a + 2a/Ö2, sus bases y a/Ö2 de altura. Por tanto
Área trapecio = (2a + 2a/√2)/2·(a/√2 ) = a2√2 + a2 = a2(1+√2 )/2 cm2.
a2(1+√2 )/2 = 3 ⇒ a2 = 6/ (1+√2 )
El área del trapecio será la suma de los cuatro trapecios, pero habremos contado ocho triángulos iguales a PPC en lugar de cuatro, pero habremos dejado de contar el cuadrado OPQR, que es igual a la suma de cuatro triángulos, por tanto, el área del octógono será, la suma de las áreas de los cuatro trapecios, es 12 cm2.
Solución 2: Área del rectángulo CDGH = (a + 2a /√2)· a = a2(1+√2) = 6/ (1+√2) · (1+√2 ) = 6 cm2.
Área del Octógono = 2 trapecios + rectángulo CDGH = 2 ·3 + 6 = 12 cm2.