En este artículo relacionaremos las medidas de los lados de un triángulo rectángulo cuyos lados son números enteros con el radio de la circunferencia inscrita recordando algunas propiedades de las ternas pitagóricas mediante el siguiente ejercicio:
Ejercicio. Si un triángulo rectángulo tiene lados números enteros, entonces el radio de la circunferencia inscrita en el triangulo también será entero.
Ternas Pitagóricas: Son tríos de números enteros positivos que dan las medidas de los lados de un triángulo rectángulo. Es decir, son tres números enteros a, b, c que cumplen que: a2 = b2 + c2 (a es la hipotenusa y b y c los catetos).
Ternas Pitagóricas Primitivas: Son las que cumplen que mcd (a, b, c) = 1
RESULTADOS DE TERNAS PITAGÓRICAS:
Resultado 1: Existen infinitas ternas pitagóricas primitivas.
Demostración: Demostraremos que cualquier número impar mayor que tres se puede poner como diferencia de los cuadrados de dos enteros consecutivos. Evidentemente:
(n+1)2 – n2 = 2n+1 ⇒ (n+1)2 = n2 + (2n+1).
Como hay infinitos impares de la forma 2n+1, entre ellos habrá infinitos impares que serán cuadrados
(para n = 4, n = 12, n = 24, n = 40, …)
Existe infinitos triángulos rectángulos cuya hipotenusa será:
a = n+1 y los catetos b = n y c = √(2n+1)
(para n = 4, n = 12, n = 24, n = 40, n = 60…)
Resultado 2: Los catetos de las ternas pitagóricas primitivas tienen diferente paridad
Demostración; Sea el triángulo rectángulo de lados a, b, c que forman una terna pitagórica primitiva, a2 = b2 + c2, donde b y c son los catetos. Veamos que los catetos a y b tienen diferente paridad
Si los catetos b y c son pares, entonces b2 y c2 serán pares ⇒ a2 ⇒ a par, por lo tanto, a, b, c son pares y mcd (a, b, c) es múltiplo de dos y, por lo tanto, a, b, c no son una terna pitagórica primitiva
Si los catetos b y c son impares, entonces b= 2m+1 y c = 2n+1
b2 + c2 = (2m+1)2 + (2n + 1)2= 4(m2 + n2 + m + n) + 2 = a2
es decir, el cuadrado de la hipotenusa es par, pero no múltiplo de 4, por tanto, no puede ser un cuadrado perfecto. De ello se deduce que los catetos de una terna pitagórica primitiva no pueden ser ambos impares. Por lo tanto, los catetos de una terna pitagórica primitiva no pueden ser de la misma paridad.
Resultado 3: La hipotenusa de una terna pitagórica primitivas es impar.
Demostración: Consecuencia inmediata del resultado anterior.
EJERCICIO: Si un triángulo rectángulo tiene lados enteros, entonces el radio
de la circunferencia inscrita al triángulo también será entero.
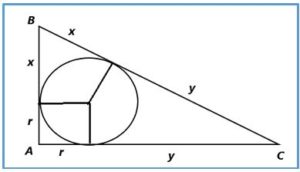
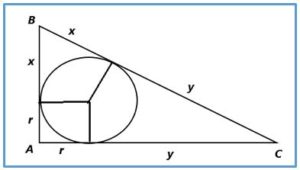
Observemos la figura con el triángulo rectángulo ABC y la circunferencia inscrita: El triángulo por ser rectángulo verifica que: a2 = b2 + c2.
Supongamos que a, b, c es una terna pitagórica primitiva De la figura se deduce que:
a = x + y, b = x + r c = y + r
Luego x = b – r y = c – r y, como a = (x + y), tenemos que:
a = (x + y) = (b – r) + (c – r) ⇒ a = b + c – 2r ⇒
![]()
Como a, b y c forman una terna pitagórica primitiva los catetos son de diferente paridad, por lo tanto, b + c será impar y la hipotenusa a impar por lo tanto a + b – a será par y, por lo tanto, el radio de la circunferencia inscrita, r, es entero, que es lo que se quería probar.




