Las leyes de las Ciencias Físicas pueden ser utilizadas en la resolución de problemas puramente matemáticos. Es cierto que la Física es una ciencia matematizada, hay cuestiones bastante simples que ponen de manifiesto la relación estrecha entre las Matemáticas y la Física y, en todo caso, cuestiones como la que veremos a continuación sorprenden y motivan. Esta relación se pone de manifiesto cuando, inspirados en superficies creadas por las burbujas de jabón, se determinan superficies mínimas y estables, que han servido de modelo sugerentes para el diseño y construcción de cubiertas de polideportivos, auditorios y teatros. La inspiración en la física ha utilizado las propiedades de la luz para resolver problemas de recorridos mínimos. Asimismo la posición de equilibrio de tres masas iguales sometidas a la ley de gravedad ha servido para determinar el Punto de Fermat de un triángulo (para calcular el punto de un triángulo tal que la suma de las distancias a los lados de un triángulo sea mínima).
Resolución de la ecuación x3 + x = c del Principio de la Hidrostática de los vasos comunicantes:
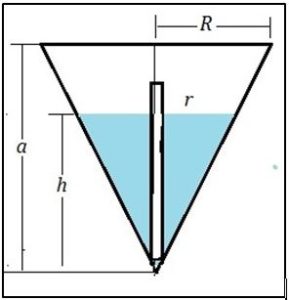
Consideremos un cilindro cuya área de la base mide 1 cm2 y un cono comunicado con él como se muestra en la figura. La relación entre el radio de la base, R, la base y la altura del recipiente cónico, a, cumple la relación siguiente:
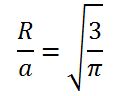Cuando vertimos c cm3 de líquido en el cilindro, por el principio de los vasos comunicantes se alcanzara una altura h en ambos recipientes, el volumen de líquido contenido en el cilindro será h cm3 (ya que la base del cilindro es 1 cm2) y el volumen de líquido contenido en el cono, como el agua adopta una forma cónica de radio r y altura h será:
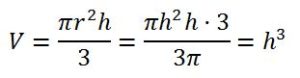
Ya que
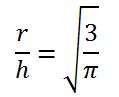
El volumen de agua contenido en el cilindro, h , junto con el volumen de agua contenido en el cono, h3 , será igual al volumen total de agua, c. Y la altura alcanzada por el agua será la solución de la ecuación propuesta, ya que verifica:
h3 + h = c
También se puede resolver la ecuación x3 – x = c por el método hidrostático (aunque con un pequeño error) introduciendo el cilindro de base un cm2, cerrado por ambas bases, (una varilla de hierro) dentro del recipiente cónico y echando una cantidad c de agua en el cono la altura h que alcanza el agua cumple que h3 – h = c y h es la ecuación de la ecuación.
