Teorema Fundamental de la Aritmética dice que todo número entero se puede descomponer de manera única (salvo el orden de los factores) en producto de factores primos.
El resultado apareció en los Elementos de Euclides en el año 300 a.C. y alcanzó su formulación definitiva con K. F. Gauss (1777-1855) el año 1801.
El libro VII de los Elementos, que consta de veintidós definiciones y treinta y nueve proposiciones, contiene dos proposiciones, la 30 y la 31, relacionadas con el Teorema Fundamental de la Aritmética (TFA) que son:
Proposición 30: Si el producto dedos números es medido por algún número primo, este número también medirá a alguno de los números iniciales.
Proposición 31: Todo número compuesto es medido por algún número primo.
En el libro IX, que trata de la Teoría de los Números, también recoge una proposición relacionada con el TFA. para la demostración de esta proposición, Euclides tiene en cuenta la definición de número primo, número compuesto y la Proposición 30 del libro VII, que es la siguiente:
Proposición 14: Si un número es el menor medido por números primos, no será medido por ningún otro número primo fuera de los que le medían desde un principio.
El matemático árabe Al Farisi (1260-1320) lo formuló en la siguiente forma:
Cada número compuesto puede necesariamente ser descompuesto en un número finito de factores primos de los cuales éste es el producto.
Finalmente Gauss le dio la formulación definitiva
Teorema. Cualquier número compuesto puede descomponerse en factores primos de una manera única
Euler (1707-1783), en el primer volimen de su obra Introducción al Álgebra (1770). sentó llos procedimientos y las operaciones fundamentales, que eran:
1.- Descomposición de un número en factores primos N = aα·bβ·c , siendo a, b y c primos
2.- Formación de todos los divisores de un número entero N
Para hallar los divisores de un número N procederemos como sigue:
2-1.- Descomponemoso N en producto de factores primos (supongamos que aparecen tres factores primos a, b y c), entonces N = ap·bq·cr
2-2.- Escribir todas las potencias de a, b y c con exponentes menores o iguales que p, q y r respectivamente:
A= {a0, a1, a2,…, ap} B={ b0, b1, b2,…, bq} C={c0, c1, c2,…, cr}
Los divisores de N se obtendrán formando todos los productos posibles de cada potencia de a por cada potencia de b y por cada potencia de c. Es decir, que cada divisor es un elemento del conjunto producto cartesiano AxBxC .
2-3.- Como consecuencia, el número de divisores de N será el número de elementos del conjunto AxBxC , es decir:
Nº de div(N) = (p+1)·(q+1)(r+1)
Euler generalizó la fórmula anterior para el caso de que N tuviera más de tres factores primos.
3-4.- La suma de los divisores de un número N de tres cifras será:
S = (1+ a1+ a2+…+ ap)·(1+ b1+ b2+…+ bq)·(1+ c1+ c2+…+ cr) =
(Aplicando la fórmula de la suma de los términos de una progresión geométrica):
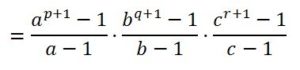
EJERCICIOS
Ejercicio 1.- Calcula el nº N = 2a· 3b, sabiendo que N2 tiene triple número de divisores que N
Solución: Número de divisores de N = 2a· 3b es (a+1)(b+1).
Número de divisores de N2 = 22a· 32b = (2a+1)(2b+1). Por lo tanto:
(2a+1)(2b+1) = 3(a+1)(b+1) ⇒ 4ab+2a+2b+1 = 3ab+3a+3b+3 ⇒
⇒ ab – a – b – 2 = 0 ⇒ a (b-1) = b +2, por lo tanto:
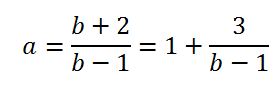
Como a y b tienen que ser enteros positivos b – 1 ≤ 3, luego caben dos posibilidades:
- – b – 1 = 1 ⇒ b = 2 y a = 4 ⇒ el número debe ser: N = 24 32
- – b – 1 = 3 ⇒ b = 4 y a = 2 ⇒ el número debe ser: N = 22 34
Ejercicio 2.- Calcula un número N = 2a· 3b ·5c, sabiendo que N/2 tiene 24 divisores menos, N/3 tiene 18 divisores menos y N/5 tiene 12 divisores menos
Solución:
(a +1)(b+1)(c+1) – (a)(b +1)(c +1) = 24 (b +1)(c+1) = 24 (1)
(a +1)(b+1)(c+1) – (a +1)(b)(c +1) = 18 (a +1)(c +1) = 18 (2)
(a +1)(b+1)(c+1) – (a +1)(b +1)(c) = 12 (a +1)(b +1) = 12 (3)
Eliminando c [Dividiendo (1) entre (2) ] resulta el sistema:
(b+1) = 4/3(a+1)
(a +1)(b +1) = 12
De donde:
4/3 (a+1)2 = 12 ⇒ (a+1)2 = 9 ⇒ a + 1 = 3 ⇒ a = 2
Sustituyendo a = 2 en (3) ⇒ 3(b+1) = 12 ⇒ b = 3
Sustituyendo a = 2 en (2) ⇒ 3(c+1) = 18 ⇒ c = 5
Luego N = 22· 33 ·55
Ejercicio 3.- Calcular la suma de los divisores de N = 22· 33 ·55
Solución: (Aplicando el resultado 3-4)
S = (1+ 21 + 22)·(1+ 31+ 32+34)·(1+ 51 + 52 +…+ 55)
![]()