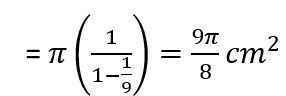
En este escrito presentaremos unos problemas geométricos en los que aplicamos algunas propiedades métricas del triángulo equilátero, fundamentalmente usaremos el hecho de que su apotema es el radio de la circunferencia inscrita y su medida es igual a la mitad del radio del mismo. Así como algunas relaciones de semejanza. Estos problemas se pueden de varias formas diferentes.
PROBLEMA 1.- Calcula el área de un triángulo equilátero cuyo radio de la circunferencia inscrita mide 2 cm.
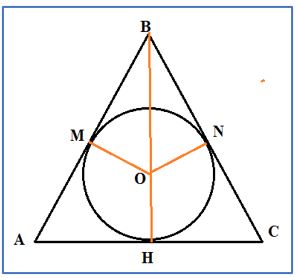
Solución: De mostraremos en primer lugar que la apotema es la mitad del radio. Sea L el lado del triángulo equilátero, a la apotema del triángulo y r el radio del triángulos y h la altura del mismo. Los haremos utilizando a propiedad de que el área del triángulo ABC es el triple del área del triángulo OAC, [OAB o OBC], por tanto:
(3·L·a)/2 = (L·h)/2 ⇒ 3a = h ⇒ a = h/3
Luego, como r = h – a ⇒ r = 2h /3 ⇒ r = 2a
Método 1: Calculemos el lado del triángulo ABC:
Consideremos el lado del triángulo rectángulo OMB:
OM = 2 cm, OB = 4 cm por el teorema de Pitágoras: MB = √12 = 2 √3 cm, por tanto:
L = AB = 4 √3 cm
Area de OMB = OM·MB/2 = 2 √3 cm2 ⇒ Area de ABC = 6· Area de OMB= 12 √3 cm2
Método 2: HB = 6, en el triángulo rectángulo ABC , llamaremos HC = x, como ABC es equilátero, BC = 2x, por el teorema de Pitágoras: (2x )2 – x2 = 36 ⇒ 3x2 = 36 ⇒ x = 2 √3, por lo tanto, AC = 4 √3. Altura = HB = 6.
El área Area de ABC = AC·BH /2 = 12 √2 cm2
Método 3: Como la apotema es la mitad del radio Considerando, por ejemplo AH , la mitad del lado AH2 = OA2 – OH2 = 16 – 4 = 12 ⇒ AH = 2 √3 ⇒ AC = 4 √3
Area de ABC = AC·BH /2 = 12 √3 cm2
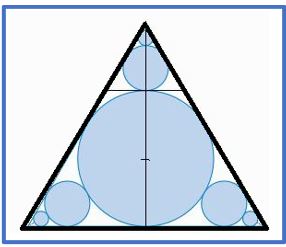
PROBLEMA 2.- Calcula el área de un triángulo equilátero cuyo radio de una de las tres circunferencias inscritas mide 2 cm.
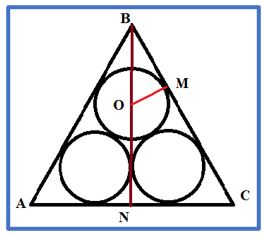
Solución: El triángulo determinado los por tres centros OO’O’’ de las tres circunferencias tiene lado 4 cm. Su área total será 2 √3
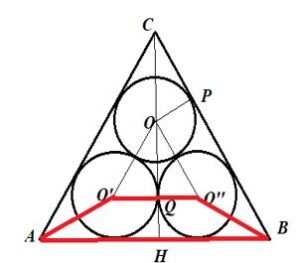
Y cada uno de los tres trapecios iguales que componen el triángulo tienen de altura 2cm, b= 4cm y B = 2 + 2Ö3, por tanto, su área será:
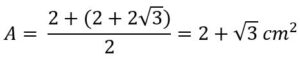
Área total 2+ 3 √3 cm2
PROBLEMA 3 .- La altura del triángulo equilátero de figura mide 3 cm. Calcula el área de la figura coloreada y la distancia PB
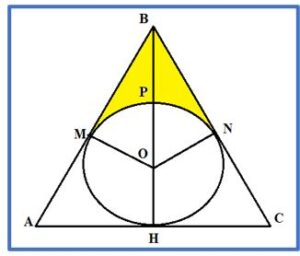
Solución: La apotema, OH, de un triángulo equilátero es la mitad del radio OB del mismo y OH + OB es la altura, por tanto,
OH = OP = PB = apotema = 1cm
Lado del triángulo 2 √3
Area = 3 √3 cm2
Problema 4.- Hallar el área ocupada por los infinitos círculos inscritos en un triángulo equilátero cuya altura es de 3 cm.
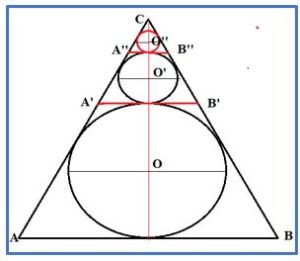
Solución: El radio del primer círculo inscrito en el triángulo ABC, será tercera parte de la altura. El segundo está inscrito en un triángulo equilátera semejante xon razón de semejanza 1/3, el siguiente 1/9 y así sucesivamente. Por lo tanto, la suma de las áreas de los círculos será:
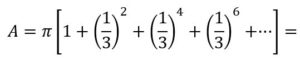
Es la suma de los términos de una progresión geométrica infinita de razón 1/9,