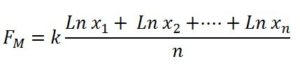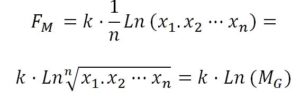La media geométrica tiene propiedades que la hacen especialmente útil en los estudios de economía, en sicología y en las ciencias sociales. En economía se emplea, por ejemplo, para calcular el promedio de porcentajes o el promedio de Índice de Precios al Consumidor (IPC) a lo largo de una serie de años.
Ejemplo: En un periodo de diez años el IPC ha subido: cuatro el 1%, dos el 4% y cuatro el 7%, ¿Cuánto ha subido en promedio el IPC en esos años?
Respuesta: El IPC indica la evolución de los precios de un conjunto de productos de consumo y de servicios representativos del gasto de una familia media de un país. Así: si el IPC ha subido el r%, significa que una familia media por cada euro que gastó el año anterior este año gastará, a = 1+ (r/100) €. Los que significa, en suma, que los gastos de la familia se han multiplicado por esa cantidad.
Por tanto, el IPC promedio de los diez años no es la media aritmética que sería:
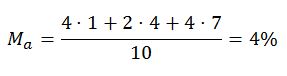
En el caso que nos ocupa los gastos en los diez años transcurridos se han multiplicado por:
(1,01)4·(1,04)2·(1,07)4 y buscamos un r fijo tal que:
(1+r)10 = (1,01)4·(1,04)2·(1,07)4 y, por tanto:
![]()
Lo que significa que el IPC habrá subido en promedio el 3,96%
Para matizar la relación de la media geométrica con los logaritmos tendremos en cuenta el siguiente resultado: El logaritmo de la media geométrica de x1, x2, x3,…, xn es la media aritmética de los logaritmos de esos números.
La comprobación es inmediata, ya que la media geométrica es:
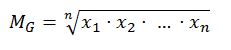
Basta tomar logaritmos y queda
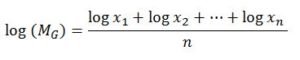
Que es lo que queríamos probar
La naturaleza logarítmica de nuestras percepciones fue enunciada en 1860 por E. H. Weber (1795-1878) y expresada en forma logarítmica pos G.T. Fechner (1801-1887). Ley de Weber-Fechner relaciona la intensidad de un estímulo con la sensación que produce. La relación no es lineal, observó que cuanto mayor fuera la intensidad del estímulo al que estemos sometidos mayor debe ser el incremento del estímulo para que podamos notar un cambio en nuestra percepción.
Lo podemos comprender recurriendo a nuestra experiencia si sopesamos con nuestra mano una masa de un kilogramo, podemos distinguirla de otra masa un kg y medio. Pero seguramente no podremos distinguirlo de una masa de un kilo y diez gramos, pero, si aumentamos progresivamente la masa, habrá un momento en que apreciaremos el incremento de peso, por ejemplo, cuando alcancemos un kilo y cincuenta gramos. Para el estímulo inicial, de un kg el umbral a partir del cual podemos discernir el cambio de masa es de cincuenta gramos. Pero el umbral no será el mismo si sopesamos una masa de 50 kilogramos. En este caso no notaremos cambio en la sensación si aumentamos cincuenta gramos o doscientos gramos, seguramente comenzaremos a sentir cambio de sensación al aumentar la masa alrededor de dos kilogramos.
Si E es la intensidad del estímulo y S es la sensación que percibimos, la ley de Weber asegura que partiendo de un estímulo de intensidad E que produce nos hace percibir una sensación S, el incremento de la sensación no es proporcional al aumento del estímulo (∆S = k· ∆E) sino que es directamente proporcional al incremento del estímulo ∆E e inversamente proporcional al estímulo E, esto es:

Integrando la ecuación diferencial obtenemos
S = k Ln E + C
Con esta formulación, se pone de manifiesto que cuando la intensidad del estímulo crece en progresión geométrica la sensación crece según una progresión aritmética, ya que (Haciendo por comodidad la constante C = 0)
Dados estímulos en progresión geométrica de razón r: E, r·E, r2E, r3E …
Para el estímulo E: S1 = k Ln E
Para el estímulo rE: S2 = k Ln rE = k (Ln r + Ln E) = k ·Ln r + k·Ln E = k ·Ln r + S1
Para el estímulo r2E S3 = k Ln r2E = k (2·Ln r + Ln E) = 2k ·Ln r + k·Ln E = 2k ·Ln r + S1
Para el estímulo r3E S4 = k Ln r3E = k (3·Ln r + Ln E) = 3k ·Ln r + k·Ln E = 3k ·Ln r + S1
….….
Luego si los estímulos siguen una progresión geométrica de razón r, las sensaciones siguen una progresión aritmética de razón k ·Ln r.
La percepción logarítmica recoge el un comportamiento destacable de la apreciación humana. A medida que aumenta el peso que soportamos con una mano observamos que necesitamos incrementos de estímulo mayores para apreciar el cambio, es decir que el umbral es cada vez más alto. Este mismo fenómeno se da también en otras sensaciones que no dependen del peso, así, por ejemplo, un año en la edad adulta pasa más deprisa que un año en la niñez, igualmente, En la percepción del sonido la relación existente entre el volumen percibido de un sonido y el volumen real sigue una ley logarítmica.
Algunos economistas han sugerido una teoría de la felicidad con clara inspiración en la percepción logarítmica también llamada teoría de la satisfacción. En la que mantienen que la felicidad no es directamente proporcional al capital o a los bienes poseídos y relacionan el binomio estímulo-sensación con el binomio dinero-nivel de satisfacción. Y llega a las expresiones:
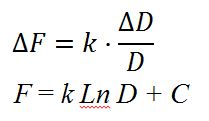
Evidentemente, si la felicidad sigue esta ley más dinero incrementa la felicidad, pero por la percepción logarítmica, pero aumentos lineales de dinero incrementan la felicidad cada vez menos. Con este criterio se puede jugar con el reparto del presupuesto global teniendo en cuenta los umbrales de percepción de cada individuo o grupo social dirigir el reparto hacia aquellos que puedan sentir con el aumento un incremento de su bienestar. Pero aplicar esto es otra historia.
Con tenemos una población de n individuos con un reparto de bienes de x1, x2, x3,…, xn, la felicidad media será proporcional (haciendo C = 0) al logaritmo de la media geométrica