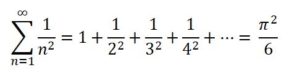Las sumas de infinitos sumandos han despertado la curiosidad de los matemáticos desde la antigüedad. Zenon de Elea (siglo V a.C.) en sus aporías planteó problemas que implicaban sumas infinitas. El manejo del infinito también llevó a los griegos a sufrir la primera crisis de la historia de las matemáticas con el descubrimiento de magnitudes inconmensurables y los números irracionales.
La Geometría Griega se apartó del infinito por las controversias que generaba. Aristóteles (384-322 a.C.) se declaró finitista en el Libro III de su Física, donde afirmaba que los matemáticos no necesitaban el infinito actual y que les bastaba con el infinito potencial. Es decir, rechazaba los conjuntos infinitos, las rectas infinitas, y los infinitesimales. Para el estagirita el geómetra podía considerar segmentos tan largos como quisiera, pero no necesitaba para nada una recta que avanzara y progresara hacia el infinito. En suma, Aristóteles admitía un atisbo de la noción de lo sería el límite en matemáticas, pero no aceptaría el trabajo con los conjuntos infinitos de Cantor.
No obstante, mediante la geometría se podían realizar sumas infinitas y era posible comprobar, haciendo uso del infinito potencial, que:
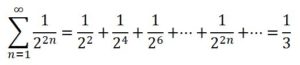
Tal y como se puede observar en la figura siguiente, en la cual un cuadrado de lado unidad se puede dividir en tres sucesiones idénticas de cuadrados de lado 1/2 , 1/4, 1/8, 1/16 …., por lo que la suma de las áreas de los cuadrados de cada una de ellas tiene que valer 1/3.
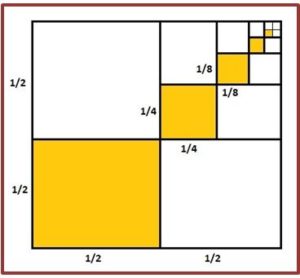
También se podía calcular por procedimientos geométricos la suma de la serie:
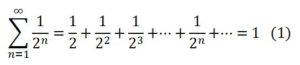
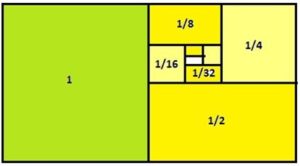
Para “calcular” geométricamente el valor de la suma partimos de un rectángulo de 2 u de largo por 1 u de ancho y que, por tanto, se puede dividir en dos cuadrados iguales. El cuadrado de la derecha, que tiene área 1u2, lo dividimos en una sucesión alternada de rectángulos semejantes al rectángulo de partida (de áreas 1/2, 1/8, ¡/32 … u2) y de cuadrados (de áreas 1/4, 1/16, ¡/64 … u2) que lo llenan completamente y cuyas áreas son, sucesivamente, los sumandos de las serie (1).
El desarrollo de la aritmética, del lenguaje algebraico y, sobre todo, del Cálculo Infinitesimal y del Análisis abrió las puestas al manejo del infinito y a poder calcular la suma de series más más complejas que las progresiones geométricas, que acabamos de ver.
Se observó que había series cuya suma era infinita, como, por ejemplo, la serie armónica que era la suma de los inversos de los números naturales (sin el cero):
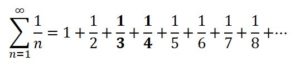
Esta serie no estaba acotada, porque, asociando los sumandos adecuadamente, como se indica a continuación, cada uno de los corchetes arrojaba una suma mayor que 1/2 :
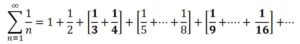
Con lo que:
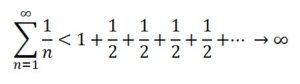
Esta demostración se basa en la propiedad siguiente: para todo número natural n se verifica que:
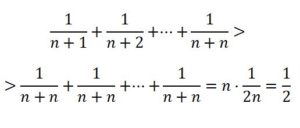
Una serie que trajo cabeza a los mejores matemáticos alrededor de cien años fue la de la suma de los inversos de los números naturales. Esta serie difícilmente se podría calcular por métodos geométricos. En 1644 el matemático P. Mengoli (1625-1686), discípulo de B. Cavalieri (1598-1647), propuso el problema de calcular la suma de los inversos de los cuadrados de los números naturales, es decir, hacer la suma:
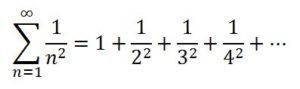
El cálculo de la suma de esta serie rebasaba con mucho las limitaciones del lenguaje geométrico para resolver cuestiones relacionadas son el infinito. Se sabía que la serie era convergente, porque se podía acotar superiormente por una serie convergente: la serie telescópica, de la siguiente forma:
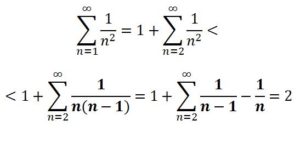
Con esa acotación se probaba que su suma era menor que dos, pero no se sabía cuánto sumaba. El problema se resistió a los mejores matemáticos. Fue popularizado por Jakob Bernoulli (1655-1705) en 1689 y lo intentaron resolver por grandes matemáticos como, Johann Bernoulli (1647-1748) o G. Leibniz (1646-1716 ), pero ninguno logró resolverlo hasta que fue abordado por el genial L. Euler (1707-1783), el cual se mostró en este caso, como en otros muchos, como un virtuoso del cálculo. El problema de calcular la suma de la serie se conoce como Problema de Basilea por ser esta la cuidad de la familia Bernoulli y de L. Euler, el cual, en su obra Introducción al análisis de los infinitos (1748), obtuvo el resultado: